
【題目】已知函數![]() .
.
(1)若曲線![]() 在
在![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的值;
的值;
(2)當![]() 且
且![]() 時,函數
時,函數![]() 的圖象總在直線
的圖象總在直線![]() 的下方,求實數
的下方,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
![]() 求出函數
求出函數![]() 的導數
的導數![]() ,由切線方程可得
,由切線方程可得![]()
![]() ,解方程即可;
,解方程即可;
![]() 由題意知,
由題意知,![]() 對任意
對任意![]() 恒成立等價于不等式
恒成立等價于不等式![]() 對任意
對任意![]() 恒成立,
恒成立,
令函數![]() ,證明
,證明![]() 在
在![]() 恒成立即可;
恒成立即可;
對函數![]() 進行求導
進行求導![]() ,利用導數
,利用導數![]() 判斷函數
判斷函數![]() 的單調性,求最值即可求出實數
的單調性,求最值即可求出實數![]() 的取值范圍.
的取值范圍.
![]() 依題意,
依題意,![]() ,
,
故![]() ,則
,則![]() ,解得
,解得![]() ;
;
![]() 依題意,當
依題意,當![]() 時,
時,![]() 恒成立,
恒成立,
即![]() 對任意
對任意![]() 恒成立,
恒成立,
令![]() ,證明
,證明![]() 在
在![]() 恒成立即可,
恒成立即可,
因為![]() ,
,
令![]() ,當
,當![]() 時,
時,![]() 圖象開口向下,
圖象開口向下,
又因為![]() 在
在![]() 上有兩個零點1和
上有兩個零點1和![]() ,
,
①當![]() 時,即
時,即![]() ,此時
,此時![]() 在
在![]() 上恒成立,
上恒成立,
![]() 函數
函數![]() 在
在![]() 上單調遞減,因為
上單調遞減,因為![]() ,
,
所以函數![]() 在
在![]() 恒成立,符合題意;
恒成立,符合題意;
②當![]() 時,即
時,即![]() ,此時當
,此時當![]() 時,
時, ![]() ,
,
![]() 函數
函數![]() 在
在![]() 上單調遞減,因為
上單調遞減,因為![]() ,
,
所以函數![]() 在
在![]() 恒成立,符合題意;
恒成立,符合題意;
③當![]() 時,即
時,即![]() ,此時當
,此時當![]() 時,
時,![]() ,
,
當![]() 時,
時, ![]() ,
,
![]() 函數
函數![]() 在
在![]() 上單調遞增;在
上單調遞增;在![]() 上單調遞減;
上單調遞減;
所以![]() ,不符合題意;
,不符合題意;
綜上可知,實數![]() 的取值范圍為
的取值范圍為![]() .
.


 活力課時同步練習冊系列答案
活力課時同步練習冊系列答案 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】某鮮花店每天制作![]() 、
、![]() 兩種鮮花共
兩種鮮花共![]() 束,每束鮮花的成本為
束,每束鮮花的成本為![]() 元,售價
元,售價![]() 元,如果當天賣不完,剩下的鮮花作廢品處理.該鮮花店發現這兩種鮮花每天都有剩余,為此整理了過往100天這兩種鮮花的日銷量(單位:束),得到如下統計數據:
元,如果當天賣不完,剩下的鮮花作廢品處理.該鮮花店發現這兩種鮮花每天都有剩余,為此整理了過往100天這兩種鮮花的日銷量(單位:束),得到如下統計數據:
| 48 | 49 | 50 | 51 |
天數 | 25 | 35 | 20 | 20 |
| 48 | 49 | 50 | 51 |
天數 | 40 | 35 | 15 | 10 |
以這100天記錄的各銷量的頻率作為各銷量的概率,假設這兩種鮮花的日銷量相互獨立.
(1)記該店這兩種鮮花每日的總銷量為![]() 束,求
束,求![]() 的分布列.
的分布列.
(2)鮮花店為了減少浪費,提升利潤,決定調查每天制作鮮花的量![]() 束.以銷售這兩種鮮花的日總利潤的期望值為決策依據,在每天所制鮮花能全部賣完與
束.以銷售這兩種鮮花的日總利潤的期望值為決策依據,在每天所制鮮花能全部賣完與![]() 之中選其一,應選哪個?
之中選其一,應選哪個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-ax-1(e為自然對數的底數),a>0.
(1)若函數f(x)恰有一個零點,證明:aa=ea-1;
(2)若f(x)≥0對任意x∈R恒成立,求實數a的取值集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四邊形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分別為BE,BP,PC的中點.
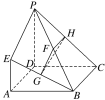
(1)求證:平面ABE⊥平面GHF;
(2)求直線GH與平面PBC所成的角θ的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 在橢圓
在橢圓![]() 上,
上,![]() 為右焦點,
為右焦點,![]() 軸,
軸,![]() 為橢圓上的四個動點,且
為橢圓上的四個動點,且![]() ,
,![]() 交于原點
交于原點![]() .
.
(1)判斷直線![]() 與橢圓的位置關系;
與橢圓的位置關系;
(2設![]() ,
,![]() 滿足
滿足![]() ,判斷
,判斷![]() 的值是否為定值,若是,請求出此定值,并求出四邊形
的值是否為定值,若是,請求出此定值,并求出四邊形![]() 面積的最大值,否則說明理由.
面積的最大值,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“二萬五千里長征”是1934年10月到1936年10月中國工農紅軍進行的一次戰略轉移,是人類歷史上的偉大奇跡,向世界展示了中國工農紅軍的堅強意志,在期間發生了許多可歌可泣的英雄故事.在中國共產黨建黨![]() 周年之際,某中學組織了“長征英雄事跡我來講”活動,已知該中學共有高中生
周年之際,某中學組織了“長征英雄事跡我來講”活動,已知該中學共有高中生![]() 名,用分層抽樣的方法從該校高中學生中抽取一個容量為
名,用分層抽樣的方法從該校高中學生中抽取一個容量為![]() 的樣本參加活動,其中高三年級抽了
的樣本參加活動,其中高三年級抽了![]() 人,高二年級抽了
人,高二年級抽了![]() 人,則該校高一年級學生人數為( )
人,則該校高一年級學生人數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)若曲線![]() 上一點
上一點![]() 的極坐標為
的極坐標為![]() ,且
,且![]() 過點
過點![]() ,求
,求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com