
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
試題分析:(1)根據二倍角公式![]() ,三角形內角和
,三角形內角和![]() ,所以
,所以![]() ,整理為關于
,整理為關于![]() 的二次方程,解得角
的二次方程,解得角![]() 的大小;(2)根據三角形的面積公式和上一問角
的大小;(2)根據三角形的面積公式和上一問角![]() ,代入后解得邊
,代入后解得邊![]() ,這樣就知道
,這樣就知道![]() ,然后根據余弦定理再求
,然后根據余弦定理再求![]() ,最后根據證得定理分別求得
,最后根據證得定理分別求得![]() 和
和![]() .
.
試題解析:(1)由cos 2A-3cos(B+C)=1,
得2cos2A+3cos A-2=0,
即(2cos A-1)(cos A+2)=0,
解得cos A=![]() 或cos A=-2(舍去).
或cos A=-2(舍去).
因為0<A<π,所以A=![]() .
.
(2)由S=![]() bcsin A=
bcsin A=![]() bc×
bc×![]() =
=![]() bc=5
bc=5![]() ,得bc=20,又b=5,知c=4.
,得bc=20,又b=5,知c=4.
由余弦定理得a2=b2+c2-2bccos A=25+16-20=21,故a=![]() .
.
從而由正弦定理得sin B sin C=![]() sin A×
sin A×![]() sin A=
sin A=![]() sin2A=
sin2A=![]() ×
×![]() =
=![]() .
.


 巧學巧練系列答案
巧學巧練系列答案科目:高中數學 來源: 題型:
【題目】若函數exf(x)(e=2.71828…,是自然對數的底數)在f(x)的定義域上單調遞增,則稱函數f(x)具有M性質,下列函數:
①f(x)=![]() (x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
(x>1) ②f(x)=x2 ③f(x)=cosx ④f(x)=2-x
中具有M性質的是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+![]() .
.
(I)當a=![]() 時,求函數f(x)在x=0處的切線方程;
時,求函數f(x)在x=0處的切線方程;
(II)函數f(x)是否存在零點?若存在,求出零點的個數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》(第二季)亮點頗多,十場比賽每場都有一首特別設計的開場詩詞,在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.若《將進酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另確定的兩首詩詞排在后六場,且《將進酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰且均不排在最后,則后六場的排法有( )
A. ![]() 種 B.
種 B. ![]() 種 C.
種 C. ![]() 種 D.
種 D. ![]() 種
種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某植物園準備建一個五邊形區域的盆栽館,三角形ABE為盆裁展示區,沿AB、AE修建觀賞長廊,四邊形BCDE是盆栽養護區,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
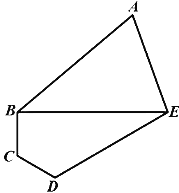
(1)求兩區域邊界BE的長度;
(2)若區域ABE為銳角三角形,求觀賞長廊總長度AB+AE的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠為檢驗車間一生產線是否工作正常,現從生產線中隨機抽取一批零件樣本,測量尺寸(單位: mm )繪成頻率分布直方圖如圖所示:
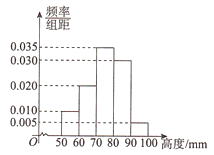
(Ⅰ)求該批零件樣本尺寸的平均數 x 和樣本方差 ![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(Ⅱ)若該批零件尺寸![]() 服從正態分布
服從正態分布 ![]() ,其中
,其中 ![]() 近似為樣本平均數
近似為樣本平均數 ![]() 近似為樣本方差
近似為樣本方差 ![]() ,利用該正態分布求
,利用該正態分布求 ![]() ;
;
(Ⅲ)若從生產線中任取一零件,測量尺寸為30mm,根據 ![]() 原則判斷該生產線是否正常?
原則判斷該生產線是否正常?
附: ![]() ;若
;若![]() ,則
,則 ![]() ,
, ![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐P-ABCD的底面ABCD是平行四邊形,PA⊥平面ABCD.M是AD的中點,N是PC的中點.
(1)求證:MN∥平面PAB;
(2)若平面PMC⊥平面PAD,求證:CM⊥AD;
(3)若平面ABCD是矩形,PA=AB,求證:平面PMC⊥平面PBC.
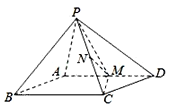
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com