分析:本題適合建立空間坐標系得用向量法解決這個立體幾何問題,建立空間坐標系,給出有關點的坐標,設出點F的坐標,(I)由線面垂直轉化為線的方向向量與面的法向量垂直,利用二者內積為零建立關于參數的方程參數.(II)求出兩平面的法向量,利用夾角公式求二面角的余弦值即可.
解答: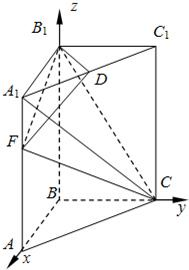
解:(1)因為直三棱柱ABC-A
1B
1C
1中,
BB
1⊥面ABC,∠ABC=
.
以B點為原點,BA、BC、BB
1分別為x、y、z軸建立如圖所示空間直角坐標系.
因為AC=2,∠ABC=90°,所以AB=BC=
,
從而B(0,0,0),A
(, 0, 0),C
(0, , 0),B
1(0,0,3),A
1(, 0, 3),C
1(0, , 3),D
(, , 3),E
(0, , ).
所以
=(, -, 3),
設AF=x,則F(
,0,x),
=(, -, x), =(, 0, x-3), =(, , 0).
•=•+(-)•+x•0=0,所以
⊥.
要使CF⊥平面B
1DF,只需CF⊥B
1F.
由
•=2+x(x-3)=0,得x=1或x=2,
故當AF=1或2時,CF⊥平面B
1DF.(5分)
(2)由(1)知平面ABC的法向量為n
1=(0,0,1).
設平面B
1CF的法向量為n=(x,y,z),則由
得
令z=1得
n=(, , 1),
所以平面B
1CF與平面ABC所成的銳二面角的余弦值
cos?n,n1>==.
點評:考查用空間向量為工具解決立體幾何問題,此類題關鍵是找清楚線的方向向量、面的法向量以及這些向量內積為0、共線等與立體幾何中線面、面面位置關系的對應.

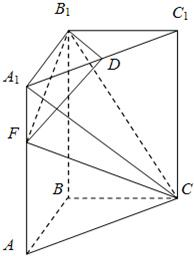 如圖,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,
如圖,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形, 解:(1)因為直三棱柱ABC-A1B1C1中,
解:(1)因為直三棱柱ABC-A1B1C1中,

 53天天練系列答案
53天天練系列答案 如圖,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=
如圖,直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB= 如圖,直三棱柱ABC-A1B1C1中,底面是以∠ABC為直角的等腰直角三角形,AC=2a,BB1=3a,D為A1C1的中點,E為B1C的中點.
如圖,直三棱柱ABC-A1B1C1中,底面是以∠ABC為直角的等腰直角三角形,AC=2a,BB1=3a,D為A1C1的中點,E為B1C的中點. 如圖,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分別為AC,B1C1的中點.
如圖,直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分別為AC,B1C1的中點. 如圖,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中點.
如圖,直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=a,AA1=2a,D棱B1B的中點.