
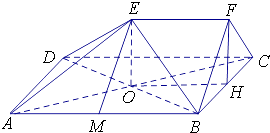
【題目】如圖,在五面體ABCDEF中,四邊形ABCD是邊長為2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= ![]() .
. 
(1)求證:AB⊥平面BCF;
(2)求直線AE與平面BDE所成角的正切值.
【答案】
(1)證明:取AB的中點M,連接EM,則AM=MB=1,
∵EF∥平面ABCD,EF平面ABEF,平面ABCD∩平面ABEF=AB,
∴EF∥AB,即EF∥MB.
∵EF=MB=1
∴四邊形EMBF是平行四邊形.
∴EM∥FB,EM=FB.
在Rt△BFC中,FB2+FC2=BC2=4,又FB=FC,得FB= ![]() .
.
∴EM= ![]() .
.
在△AEM中,AE= ![]() ,AM=1,EM=
,AM=1,EM= ![]() ,
,
∴AM2+EM2=3=AE2,
∴AM⊥EM.
∴AM⊥FB,即AB⊥FB.
∵四邊形ABCD是正方形,
∴AB⊥BC.
∵FB∩BC=B,FB平面BCF,BC平面BCF,
∴AB⊥平面BCF.
(2)解:連接AC,AC與BD相交于點O,則點O是AC的中點,
取BC的中點H,連接OH,EO,FH,
則OH∥AB,OH= ![]() AB=1.
AB=1.
由(1)知EF∥AB,且EF= ![]() AB,
AB,
∴EF∥OH,且EF=OH.
∴四邊形EOHF是平行四邊形.
∴E0∥FH,且EO=FH=1.
由(1)知AB⊥平面BCF,又FH平面BCF,
∴FH⊥AB,
∵FH⊥BC,AB∩BC=B,FH平面ABCD,BC平面ABCD,
∴FH⊥平面ABCD.
∴E0⊥平面ABCD.
∵AO平面ABCD,
∴EO⊥AO.
∵AO⊥BD,EO∩BD=O,EO平面EBD,BD平面EBD,
∴AO⊥平面EBD.
∴∠AEO是直線AE與平面BDE所成的角.
在Rt△AOE中,tan∠AEO= ![]() =
= ![]() .
.
∴直線AE與平面BDE所成角的正切值為 ![]() .
.
【解析】(1)先證明出四邊形EMBF是平行四邊形,推斷出EM∥FB,EM=FB.進而在Rt△BFC中求得EM,在△AEM中,根據邊長推斷出AM2+EM2=3=AE2 , 進而證明出AM⊥EM.然后證明出四邊形ABCD是正方形,進而推斷出AB⊥BC.最后通過線面垂直的判定定理證明出AB⊥平面BCF.(2)先證明出∠AEO是直線AE與平面BDE所成的角,進而在Rt△AOE中,求得tan∠AEO.
【考點精析】通過靈活運用直線與平面垂直的判定和空間角的異面直線所成的角,掌握一條直線與一個平面內的兩條相交直線都垂直,則該直線與此平面垂直;注意點:a)定理中的“兩條相交直線”這一條件不可忽視;b)定理體現了“直線與平面垂直”與“直線與直線垂直”互相轉化的數學思想;已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則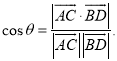 即可以解答此題.
即可以解答此題.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,直線PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4. 
(1)求證:直線DE⊥平面PAC.
(2)若直線PE與平面PAC所成的角的正弦值為 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|. (Ⅰ)若不等式f(x)≤2的解集為[0,4],求實數a的值;
(Ⅱ)在(Ⅰ)的條件下,若x0∈R,使得f(x0)+f(x0+5)﹣m2<4m,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,0),若函數f(x)的圖象上存在兩點B、C到點A的距離相等,則稱該函數f(x)為“點距函數”,給定下列三個函數:①y=﹣x+2;② ![]() ;③y=x+1.其中,“點距函數”的個數是( )
;③y=x+1.其中,“點距函數”的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,D為BC的中點,∠BAD+∠C≥90°. (Ⅰ)求證:sin2C≤sin2B;
(Ⅱ)若cos∠BAD=﹣ ![]() ,AB=2,AD=3,求AC.
,AB=2,AD=3,求AC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com