
【題目】在平面直角坐標系![]() 中有如下正確結(jié)論:
中有如下正確結(jié)論:![]() 為曲線
為曲線![]() (
(![]() 、
、![]() 為非零實數(shù),且不同時為負)上一點,則過點
為非零實數(shù),且不同時為負)上一點,則過點![]() 的切線方程為
的切線方程為![]() .
.
(1)已知![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為過點
為過點![]() 的橢圓的切線,若直線
的橢圓的切線,若直線![]() 與直線
與直線![]() 的斜率分別為
的斜率分別為![]() 與
與![]() ,求證:
,求證:![]() 為定值;
為定值;
(2)過橢圓![]() 上一點
上一點![]() 引橢圓
引橢圓![]() 的切線,與
的切線,與![]() 軸交于點
軸交于點![]() .若
.若![]() 為正三角形,求橢圓
為正三角形,求橢圓![]() 的方程;
的方程;
(3)求與圓![]() 及(2)中的橢圓
及(2)中的橢圓![]() 均相切的直線
均相切的直線![]() 與坐標軸圍成的三角形的面積的取值范圍.
與坐標軸圍成的三角形的面積的取值范圍.
【答案】(1)證明見解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據(jù)已知題目中所給的結(jié)論結(jié)合斜率公式可以證明出![]() 為定值;
為定值;
(2) 由題目中的結(jié)論求出橢圓切線方程,求出點![]() 的坐標,根據(jù)等邊三角形三邊相等列出方程組,即可求出
的坐標,根據(jù)等邊三角形三邊相等列出方程組,即可求出![]() 的值;
的值;
(3)設(shè)出直線![]() 的方程,根據(jù)與圓
的方程,根據(jù)與圓![]() 相切和(2)中橢圓相切,得到兩個等式,求出三角形的面積表達式,最后利用基本不等式可以求出三角形的面積的取值范圍.
相切和(2)中橢圓相切,得到兩個等式,求出三角形的面積表達式,最后利用基本不等式可以求出三角形的面積的取值范圍.
(1) ![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為過點
為過點![]() 的橢圓的切線,所以
的橢圓的切線,所以![]() 的方程為:
的方程為:![]() ,由題意可知:
,由題意可知:![]() ,所以
,所以 ![]()
![]() 為定值;
為定值;
(2)設(shè)點![]() 的坐標為:
的坐標為:![]() ,由已知所給的結(jié)論可知:過橢圓
,由已知所給的結(jié)論可知:過橢圓![]() 上一點
上一點![]() 引橢圓
引橢圓![]() 的切線的方程為:
的切線的方程為:![]() ,與題意可知:點
,與題意可知:點![]() 的坐標為:
的坐標為:![]() .
.
 .
.
因為![]() 為正三角形,所以三邊相等,因此有方程組:
為正三角形,所以三邊相等,因此有方程組:
 ,因為點
,因為點![]() 在橢圓上,所以
在橢圓上,所以
![]() 橢圓
橢圓![]() 的方程為
的方程為![]() ;
;
(3)設(shè)直線![]() 的方程為:
的方程為:![]() ,由題意可知:
,由題意可知:![]() .與兩個坐標軸的交點坐標分別為:
.與兩個坐標軸的交點坐標分別為:![]() ,所以直線
,所以直線![]() 與坐標軸圍成的三角形的面積為:
與坐標軸圍成的三角形的面積為:![]() .
.
因為直線![]() 與
與![]() 相切,所以方程組:
相切,所以方程組:![]() 有唯一解,
有唯一解,
即方程![]() 有唯一實根,故
有唯一實根,故![]() ,
,
即![]() .
.
因為直線![]() 與
與![]() 相切,所以方程組:
相切,所以方程組: 有唯一解,
有唯一解,
即方程![]() 有唯一實根,故
有唯一實根,故![]() ,
,
即![]() ,而
,而![]() ,所以
,所以![]()
因為![]() ,所以
,所以![]() ,因為
,因為![]() ,所以這個不等式恒成立.
,所以這個不等式恒成立.
 (當且僅當
(當且僅當![]() 時取等號,即
時取等號,即
![]() 取等號),所以直線
取等號),所以直線![]() 與坐標軸圍成的三角形的面積的取值范圍為
與坐標軸圍成的三角形的面積的取值范圍為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】動點![]() 與點
與點![]() 的距離和它到直線
的距離和它到直線![]() 的距離相等,記點
的距離相等,記點![]() 的軌跡為曲線
的軌跡為曲線![]()
(1)求曲線![]() 的方程
的方程
(2)設(shè)點![]() ,動點
,動點![]() 在曲線
在曲線![]() 上運動時,
上運動時,![]() 的最短距離為
的最短距離為![]() ,求
,求![]() 的值以及取到最小值時點
的值以及取到最小值時點![]() 的坐標
的坐標
(3)設(shè)![]() 為曲線
為曲線![]() 的任意兩點,滿足
的任意兩點,滿足![]() (
(![]() 為原點),試問直線
為原點),試問直線![]() 是否恒過一個定點?如果是,求出定點坐標;如果不是,說明理由
是否恒過一個定點?如果是,求出定點坐標;如果不是,說明理由
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 滿足:
滿足: ![]() ,
, 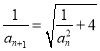 ,
, ![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設(shè)數(shù)列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() ,試確定
,試確定![]() 的值,使得數(shù)列
的值,使得數(shù)列![]() 為等差數(shù)列;
為等差數(shù)列;
(3)將數(shù)列![]() 中的部分項按原來順序構(gòu)成新數(shù)列
中的部分項按原來順序構(gòu)成新數(shù)列![]() ,且
,且![]() ,求證:存在無數(shù)個滿足條件的無窮等比數(shù)列
,求證:存在無數(shù)個滿足條件的無窮等比數(shù)列![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為保護農(nóng)民種糧收益,促進糧食生產(chǎn),確保國家糧食安全,調(diào)動廣大農(nóng)民糧食生產(chǎn)的積極性,從2004年開始,國家實施了對種糧農(nóng)民直接補貼.通過對2014~2018年的數(shù)據(jù)進行調(diào)查,發(fā)現(xiàn)某地區(qū)發(fā)放糧食補貼額![]() (億元)與該地區(qū)糧食產(chǎn)量
(億元)與該地區(qū)糧食產(chǎn)量![]() (萬億噸)之間存在著線性相關(guān)關(guān)系.統(tǒng)計數(shù)據(jù)如下表:
(萬億噸)之間存在著線性相關(guān)關(guān)系.統(tǒng)計數(shù)據(jù)如下表:
年份 | 2014年 | 2015年 | 2016年 | 2017年 | 2018年 |
補貼額 | 9 | 10 | 12 | 11 | 8 |
糧食產(chǎn)量 | 23 | 25 | 30 | 26 | 21 |
(1)請根據(jù)如表所給的數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸直線方程
的線性回歸直線方程![]() ;
;
(2)通過對該地區(qū)糧食產(chǎn)量的分析研究,計劃2019年在該地區(qū)發(fā)放糧食補貼額7億元,請根據(jù)(1)中所得的線性回歸直線方程,預(yù)測2019年該地區(qū)的糧食產(chǎn)量.
(參考公式: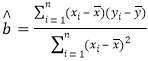 ,
,![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于曲線C所在平面上的定點![]() ,若存在以點
,若存在以點![]() 為頂點的角
為頂點的角![]() ,使得
,使得![]() 對于曲線C上的任意兩個不同的點A,B恒成立,則稱角
對于曲線C上的任意兩個不同的點A,B恒成立,則稱角![]() 為曲線C相對于點
為曲線C相對于點![]() 的“界角”,并稱其中最小的“界角”為曲線C相對于點
的“界角”,并稱其中最小的“界角”為曲線C相對于點![]() 的“確界角”.曲線
的“確界角”.曲線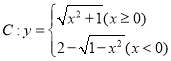 相對于坐標原點
相對于坐標原點![]() 的“確界角”的大小是 _________.
的“確界角”的大小是 _________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某高科技企業(yè)研制出一種型號為A的精密數(shù)控車床,A型車床為企業(yè)創(chuàng)造的價值逐年減少(以投產(chǎn)一年的年初到下一年的年初為A型車床所創(chuàng)造價值的第一年).若第 1 年A型車床創(chuàng)造的價值是250萬元,且第1年至第6年,每年A型車床創(chuàng)造的價值減少30萬元;從第7年開始,每年A型車床創(chuàng)造的價值是上一年價值的 50%.現(xiàn)用![]() (
(![]() )表示A型車床在第n年創(chuàng)造的價值.
)表示A型車床在第n年創(chuàng)造的價值.
(1)求數(shù)列![]() 的通項公式
的通項公式![]() ;
;
(2)記![]() 為數(shù)列
為數(shù)列![]() 的前n項的和
的前n項的和![]()
![]() ,企業(yè)經(jīng)過成本核算,若
,企業(yè)經(jīng)過成本核算,若![]() 萬元,則繼續(xù)使用A型車床,否則更換A型車床,試問該企業(yè)須在第幾年年初更換A型車床?(已知:若正數(shù)數(shù)列
萬元,則繼續(xù)使用A型車床,否則更換A型車床,試問該企業(yè)須在第幾年年初更換A型車床?(已知:若正數(shù)數(shù)列![]() 是單調(diào)遞減數(shù)列,則數(shù)列
是單調(diào)遞減數(shù)列,則數(shù)列![]() 也是單調(diào)遞減數(shù)列).
也是單調(diào)遞減數(shù)列).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,以原點為圓心,橢圓的短半軸為半徑的圓與直線
,以原點為圓心,橢圓的短半軸為半徑的圓與直線![]() 相切.
相切.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)![]() ,
,![]() ,
,![]() 是橢圓
是橢圓![]() 上關(guān)于
上關(guān)于![]() 軸對稱的任意兩個不同的點,連結(jié)
軸對稱的任意兩個不同的點,連結(jié)![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() ,證明直線
,證明直線![]() 與
與![]() 軸相交于定點
軸相交于定點![]() ;
;
(Ⅲ)在(Ⅱ)的條件下,過點![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某種植園在芒果臨近成熟時,隨機從一些芒果樹上摘下100個芒果,其質(zhì)量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經(jīng)統(tǒng)計得頻率分布直方圖如圖所示.
(單位:克)中,經(jīng)統(tǒng)計得頻率分布直方圖如圖所示.

(1) 經(jīng)計算估計這組數(shù)據(jù)的中位數(shù);
(2)現(xiàn)按分層抽樣從質(zhì)量為![]() ,
,![]() 的芒果中隨機抽取
的芒果中隨機抽取![]() 個,再從這
個,再從這![]() 個中隨機抽取
個中隨機抽取![]() 個,求這
個,求這![]() 個芒果中恰有
個芒果中恰有![]() 個在
個在![]() 內(nèi)的概率.
內(nèi)的概率.
(3)某經(jīng)銷商來收購芒果,以各組數(shù)據(jù)的中間數(shù)代表這組數(shù)據(jù)的平均值,用樣本估計總體,該種植園中還未摘下的芒果大約還有![]() 個,經(jīng)銷商提出如下兩種收購方案:
個,經(jīng)銷商提出如下兩種收購方案:
A:所以芒果以![]() 元/千克收購;
元/千克收購;
B:對質(zhì)量低于![]() 克的芒果以
克的芒果以![]() 元/個收購,高于或等于
元/個收購,高于或等于![]() 克的以
克的以![]() 元/個收購.
元/個收購.
通過計算確定種植園選擇哪種方案獲利更多?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】上海市普通高中學(xué)業(yè)水平等級考成績共分為五等十一級,各等級換算成分數(shù)如表所示:
等級 |
| A |
| B |
|
| C |
|
| D | E |
分數(shù) | 70 | 67 | 64 | 61 | 58 | 55 | 52 | 49 | 46 | 43 | 40 |
上海某高中2018屆高三![]() 班選考物理學(xué)業(yè)水平等級考的學(xué)生中,有5人取得
班選考物理學(xué)業(yè)水平等級考的學(xué)生中,有5人取得![]() 成績,其他人的成績至少是B級及以上,平均分是64分,這個班級選考物理學(xué)業(yè)水平等級考的人數(shù)至少為______人
成績,其他人的成績至少是B級及以上,平均分是64分,這個班級選考物理學(xué)業(yè)水平等級考的人數(shù)至少為______人![]()
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com