
【題目】設(shè)函數(shù)![]() ,其中
,其中![]() .
.
(![]() )若
)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)遞減區(qū)間.
的單調(diào)遞減區(qū)間.
(![]() )求函數(shù)
)求函數(shù)![]() 的極值.
的極值.
(![]() )若函數(shù)
)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上恰有兩個零點(diǎn),求
上恰有兩個零點(diǎn),求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)當(dāng)
;(2)當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 無極值,當(dāng)
無極值,當(dāng)![]() 時,
時,![]() 的極大值為
的極大值為![]() ,無極小值;(3)
,無極小值;(3)![]() .
.
【解析】試題分析:(1)求出![]() ,在定義域內(nèi),分別令
,在定義域內(nèi),分別令![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 增區(qū)間,
增區(qū)間,![]() 求得
求得![]() 的范圍,可得函數(shù)
的范圍,可得函數(shù)![]() 的減區(qū)間;(2)討論當(dāng)
的減區(qū)間;(2)討論當(dāng)![]() 時,當(dāng)
時,當(dāng)![]() 時,兩種情況,分別判斷導(dǎo)函數(shù)的符號,可得函數(shù)的單調(diào)區(qū)間,結(jié)合函數(shù)的單調(diào)性可得函數(shù)
時,兩種情況,分別判斷導(dǎo)函數(shù)的符號,可得函數(shù)的單調(diào)區(qū)間,結(jié)合函數(shù)的單調(diào)性可得函數(shù)![]() 的極值;(
的極值;(![]() )若
)若![]() 在
在![]() 恰有兩個零點(diǎn),則
恰有兩個零點(diǎn),則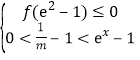 ,即
,即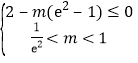 ,解得
,解得![]() .
.
試題解析:(![]() )依題意,函數(shù)
)依題意,函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,
,![]() ,令
,令![]() ,得
,得![]() ,解得
,解得![]() 或
或![]() ,又∵
,又∵![]() ,∴函數(shù)
,∴函數(shù)![]() 的單調(diào)遞減區(qū)間是
的單調(diào)遞減區(qū)間是![]() .
.
(![]() )
)![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() 恒成立,∴
恒成立,∴![]() 在
在![]() 上單調(diào)遞增,∴
上單調(diào)遞增,∴![]() 無極值,當(dāng)
無極值,當(dāng)![]() 時,
時,![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,∴
上單調(diào)遞減,∴![]() ,無極小值, 綜上所述,當(dāng)
,無極小值, 綜上所述,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 無極值,
無極值,
當(dāng)![]() 時,
時,![]() 的極大值為
的極大值為![]() ,無極小值.
,無極小值.
(![]() )由(
)由(![]() )可知,當(dāng)
)可知,當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上是增函數(shù),顯然,
上是增函數(shù),顯然,![]() 在區(qū)間
在區(qū)間![]() 不可能恰有兩個零點(diǎn),當(dāng)
不可能恰有兩個零點(diǎn),當(dāng)![]() 時,
時,![]() ,又
,又![]() , ∴
, ∴![]() 為
為![]() 的一個零點(diǎn),∴若
的一個零點(diǎn),∴若![]() 在
在![]() 恰有兩個零點(diǎn),則
恰有兩個零點(diǎn),則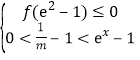 ,即
,即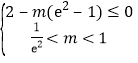 ,解得
,解得![]() .
.


 字詞句篇與同步作文達(dá)標(biāo)系列答案
字詞句篇與同步作文達(dá)標(biāo)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,已知2(tanA+tanB)= ![]() .
.
(1)證明:a+b=2c;
(2)求cosC的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于每項(xiàng)均是正整數(shù)的數(shù)列A:a1,a2,…,an,定義變換T1,T1將數(shù)列A變換成數(shù)列T1(A):n,a1-1,a2-1,…,an-1.對于每項(xiàng)均是非負(fù)整數(shù)的數(shù)列B:b1,b2,…,bm,定義變換T2,T2將數(shù)列B各項(xiàng)從大到小排列,然后去掉所有為零的項(xiàng),得到數(shù)列T2(B).又定義S(B)=2(b1+2b2+…+mbm)+![]() +
+![]() +…+
+…+![]() .設(shè)A0是每項(xiàng)均為正整數(shù)的有窮數(shù)列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
.設(shè)A0是每項(xiàng)均為正整數(shù)的有窮數(shù)列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
(1)如果數(shù)列A0為2,6,4,8,寫出數(shù)列A1,A2;
(2)對于每項(xiàng)均是正整數(shù)的有窮數(shù)列A,證明:S(T1(A))=S(A);
(3)證明:對于任意給定的每項(xiàng)均為正整數(shù)的有窮數(shù)列A0,存在正整數(shù)K,當(dāng)k≥K時,S(Ak+1)=S(Ak).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)學(xué)家歐拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直線上,且重心到外心的距離是重心到垂心距離的一半,這條直線后人稱之為三角形的歐拉線.已知![]() 的頂點(diǎn)
的頂點(diǎn)![]() ,若其歐拉線方程為
,若其歐拉線方程為![]() ,則頂點(diǎn)C的坐標(biāo)是()
,則頂點(diǎn)C的坐標(biāo)是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a∈R,函數(shù)f(x)=log2( ![]() +a).
+a).
(1)當(dāng)a=5時,解不等式f(x)>0;
(2)若關(guān)于x的方程f(x)﹣log2[(a﹣4)x+2a﹣5]=0的解集中恰好有一個元素,求a的取值范圍.
(3)設(shè)a>0,若對任意t∈[ ![]() ,1],函數(shù)f(x)在區(qū)間[t,t+1]上的最大值與最小值的差不超過1,求a的取值范圍.
,1],函數(shù)f(x)在區(qū)間[t,t+1]上的最大值與最小值的差不超過1,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=(2-a)x-2(1+ln x)+a,若函數(shù)f(x)在區(qū)間![]() 上無零點(diǎn),求實(shí)數(shù)a的最小值.
上無零點(diǎn),求實(shí)數(shù)a的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】據(jù)市場調(diào)查發(fā)現(xiàn),某種產(chǎn)品在投放市場的30天中,其銷售價格![]() (元)和時間
(元)和時間![]() (天)的關(guān)系如圖所示.
(天)的關(guān)系如圖所示.

(1)求銷售價格![]() (元)和時間
(元)和時間![]() (天)的函數(shù)關(guān)系式;
(天)的函數(shù)關(guān)系式;
(2)若日銷售量![]() (件)與時間
(件)與時間![]() (天)的函數(shù)關(guān)系式是
(天)的函數(shù)關(guān)系式是![]()
![]() ,問該產(chǎn)品投放市場第幾天時,日銷售額
,問該產(chǎn)品投放市場第幾天時,日銷售額![]() (元)最高,且最高為多少元?
(元)最高,且最高為多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2![]() ,AA1=
,AA1=![]() ,BB1=2
,BB1=2![]() ,點(diǎn)E和F分別為BC和A1C的中點(diǎn).
,點(diǎn)E和F分別為BC和A1C的中點(diǎn).

(1)求證:EF∥平面A1B1BA;
(2)求直線A1B1與平面BCB1所成角的大小.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com