
【題目】在△ABC中,A,B,C的對邊分別是a,b,c,且bcosB是acosC,ccosA的等差中項.
(1)求∠B的大小;
(2)若a+c= ![]() ,求△ABC的面積.
,求△ABC的面積.
【答案】
(1)解:∵bcosB是acosC,ccosA的等差中項,
∴acosC+ccosA=2bcosB,
由正弦定理,得sinAcosC+cosAsinC=2sinBcosB,
即sin(A+C)=2sinBcosB,
∵A+C=π﹣B,0<B<π,
∴sin(A+C)=sinB≠0,
∴cosB= ![]() ,B=
,B= ![]()
(2)解:由B= ![]() ,得
,得 ![]() =
= ![]() ,
,
即 ![]() ,
,
∴ac=2,
∴ ![]()
【解析】(1)利用等差中項的性質,知acosC+ccosA=2bcosB,由正弦定理,得sinAcosC+cosAsinC=2sinBcosB,由此結合三角函數的性質能夠求出∠B.(2)由(1)知B= ![]() ,利用余弦定理得到
,利用余弦定理得到 ![]() =
= ![]() ,再利用三角形面積公式
,再利用三角形面積公式 ![]() ,能求出△ABC的面積.
,能求出△ABC的面積.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)在R上的導函數為f′(x),若f(x)<2f′(x)恒成立,且f(ln4)=2,則不等式f(x)>e ![]() 的解集是( )
的解集是( )
A.(ln2,+∞)
B.(2ln2,+∞)
C.(﹣∞,ln2)
D.(﹣∞,2ln2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)= ![]() (x>0),觀察:
(x>0),觀察:
f1(x)=f(x)= ![]() ,
,
f2(x)=f(f1(x))= ![]() ;
;
f3(x)=f(f2(x))= ![]() .
.
f4(x)=f(f3(x))= ![]()
…
根據以上事實,當n∈N*時,由歸納推理可得:fn(1)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 分別為橢圓C:
分別為橢圓C:![]() 的左、右焦點,點
的左、右焦點,點![]() 在橢圓上,且
在橢圓上,且![]() 軸,
軸,![]() 的周長為6.
的周長為6.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)E,F是橢圓C上異于點![]() 的兩個動點,如果直線PE與直線PF的傾斜角互補,證明:直線EF的斜率為定值,并求出這個定值.
的兩個動點,如果直線PE與直線PF的傾斜角互補,證明:直線EF的斜率為定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知點A(-1,-2),B(1,3),P為x軸上的一點,求|PA|+|PB|的最小值;
(2)已知點A(2,2),B(3,4),P為x軸上一點,求||PB|-|PA||的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正項數列{an}的前n項和為Sn,且an和Sn滿足:4Sn=(an+1)2 (n=1,2,3……),
(1)求{an}的通項公式;(2)設bn=![]() ,求{bn}的前n項和Tn;
,求{bn}的前n項和Tn;
(3)在(2)的條件下,對任意n∈N*,Tn![]() 都成立,求整數m的最大值.
都成立,求整數m的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在路邊安裝路燈,燈柱![]() 的高為
的高為![]() 米,路寬
米,路寬![]() 為23米,燈桿
為23米,燈桿![]() 與燈柱
與燈柱![]() 角,路燈采用錐形燈罩,燈罩軸線
角,路燈采用錐形燈罩,燈罩軸線![]() 與燈桿
與燈桿![]() 垂直,請你建立適當直角坐標系,解決以下問題:
垂直,請你建立適當直角坐標系,解決以下問題:
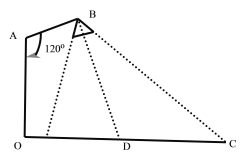
(1)當![]()
(2)![]() 且燈罩軸線
且燈罩軸線![]() 正好通過道路路面的中線時,求燈桿
正好通過道路路面的中線時,求燈桿![]() 的長為多少米?
的長為多少米?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C1:y2=2px(p>0)的焦點為F,拋物線上存在一點G到焦點的距離為3,且點G在圓C:x2+y2=9上. (Ⅰ)求拋物線C1的方程;
(Ⅱ)已知橢圓C2: ![]() =1(m>n>0)的一個焦點與拋物線C1的焦點重合,且離心率為
=1(m>n>0)的一個焦點與拋物線C1的焦點重合,且離心率為 ![]() .直線l:y=kx﹣4交橢圓C2于A、B兩個不同的點,若原點O在以線段AB為直徑的圓的外部,求k的取值范圍.
.直線l:y=kx﹣4交橢圓C2于A、B兩個不同的點,若原點O在以線段AB為直徑的圓的外部,求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com