
【題目】如圖,在三棱柱![]() 中,
中,![]() ,D,E分別是
,D,E分別是![]() 的中點.
的中點.
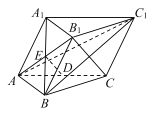
(1)求證:DE∥平面![]()
(2)若![]() ,求證:平面
,求證:平面![]() 平面
平面![]() .
.
【答案】(1)見證明;(2)見證明
【解析】
(1)連結AB1,B1C,推導出四邊形ABB1A1是平行四邊形,DE∥B1C,由此能證明DE∥平面BCC1B1.
(2)推導出DE∥B1C,從而AB⊥B1C,推導出平行四邊形BCC1B1是菱形,從而BC1⊥B1C,再由AB⊥B1C,得BC1⊥平面ABC1,由此能證明平面ABC1⊥平面BCC1B1.
(1)連結![]() .
.
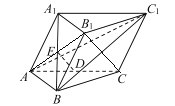
在三棱柱![]() 中,
中,![]() ,且
,且![]() ,
,
所以四邊形![]() 是平行四邊形,
是平行四邊形,
因為E是![]() 的中點,
的中點,
所以E也是![]() 中點,
中點,
又因為D是AC的中點,
所以![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以DE∥平面![]() .
.
(2) 由(1)知![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
在三棱柱![]() 中,
中,![]() ,四邊形
,四邊形![]() 是平行四邊形,
是平行四邊形,
因為![]() ,所以
,所以![]() ,
,
所以平行四邊形![]() 是菱形,
是菱形,
所以![]() ,
,
又因為![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
又因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.


科目:高中數學 來源: 題型:
【題目】
在平面直角坐標系xOy中,曲線C的參數方程為![]() (a為參數),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為
(a為參數),在以原點為極點,x軸正半軸為極軸的極坐標系中,直線l的極坐標方程為![]() .
.
(1)求C的普通方程和l的傾斜角;
(2)設點![]() ,l和C交于A,B兩點,求
,l和C交于A,B兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設甲、乙兩人每次射擊命中目標的概率分別為![]() 和
和![]() ,且各次射擊互相獨立.
,且各次射擊互相獨立.
(1)若甲、乙兩人各射擊1次,求至少有一人命中目標的概率;
(2)若甲連續射擊3次,設命中目標次數為![]() ,求命中目標次數
,求命中目標次數![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知多面體ABCDEF中,四邊形ABFE為正方形,![]() ,
,![]() ,G為AB的中點,
,G為AB的中點,![]() .
.
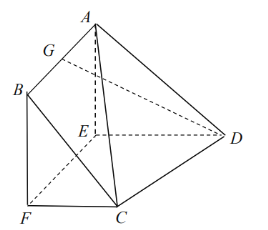
(1)求證:![]() 平面CDEF;
平面CDEF;
(2)求平面ACD與平面BCF所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假定某射手每次射擊命中的概率為![]() ,且只有3發子彈.該射手一旦射中目標,就停止射擊,否則就一直獨立地射擊到子彈用完.設耗用子彈數為X,求:
,且只有3發子彈.該射手一旦射中目標,就停止射擊,否則就一直獨立地射擊到子彈用完.設耗用子彈數為X,求:
(1)目標被擊中的概率;
(2)X的概率分布列;
(3)均值![]() ,方差V(X).
,方差V(X).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班50名學生期中考試數學成績的頻率分布直方圖如圖所示,其中成績分組區間是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].從樣本成績不低于80分的學生中隨機選取2人,記這2人成績在90分以上(含90分)的人數為ξ,則ξ的數學期望為( )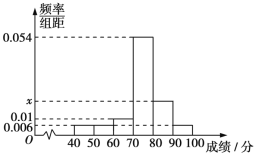
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市旅游管理部門為提升該市26個旅游景點的服務質量,對該市26個旅游景點的交通、安全、環保、衛生、管理五項指標進行評分,每項評分最低分0分,最高分100分,每個景點總分為這五項得分之和,根據考核評分結果,繪制交通得分與安全得分散點圖、交通得分與景點總分散點圖如下:
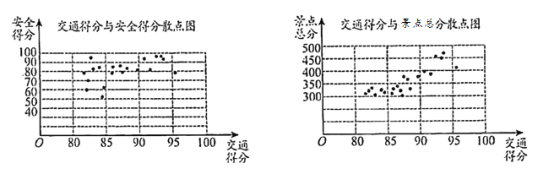
請根據圖中所提供的信息,完成下列問題:
(I)若從交通得分前6名的景點中任取2個,求其安全得分都大于90分的概率;
(II)若從景點總分排名前6名的景點中任取3個,記安全得分不大于90分的景點個數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和數學期望;
的分布列和數學期望;
(III)記該市26個景點的交通平均得分為![]() 安全平均得分為
安全平均得分為![]() ,寫出
,寫出![]() 和
和![]() 的大小關系?(只寫出結果)
的大小關系?(只寫出結果)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》是我國古老的天文學和數學著作,其書中記載:一年有二十四個節氣,每個節氣晷長損益相同(晷是按照日影測定時刻的儀器,晷長即為所測影子的長度),夏至、小暑、大暑、立秋、處暑、白露、秋分、寒露、霜降是連續的九個節氣,其晷長依次成等差數列,經記錄測算,這九個節氣的所有晷長之和為49.5尺,夏至、大暑、處暑三個節氣晷長之和為10.5尺,則立秋的晷長為( )
A.1.5尺B.2.5尺C.3.5尺D.4.5尺
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com