設函數f(x)=x(x-a)2,
(I)證明:a<3是函數f(x)在區間(1,2)上遞減的必要而不充分的條件;
(II)若x∈[0,|a|+1]時,f(x)<2a2恒成立,且f(0)=0,求實數a的取值范圍.
【答案】
分析:(I)先求函數f(x)在區間(1,2)上遞減的充要條件,
f(x)在區間(1,2)上遞減?f'(x)=3x
2-4ax+a
2≤0在區間(1,2)上恒成立,處理二次不等式恒成立問題可用實根分布求解.
(II)x∈[0,|a|+1]時,f(x)<2a
2恒成立?f(x)
max<2a
2,x∈[0,|a|+1],問題轉化為求函數的最值問題.
解答:解:(I)∵f(x)在區間(1,2)上遞減,
∴其導函數f'(x)=3x
2-4ax+a
2≤0在區間(1,2)上恒成立.
∴
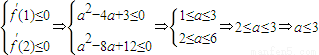
故a≤3是函數f(x)在區間(1,2)上遞減的必要而不充分的條件
解法二:f'(x)=3x
2-4ax+a
2=(3x-a)(x-a)≤0在區間(1,2)上恒成立,
∴a只能大于0,∴
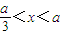
,∴
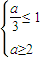
∴2≤a≤3⇒a≤3
故a≤3是函數f(x)在區間(1,2)上遞減的必要而不充分的條件
(II)∵f(x)=x(x-a)
2
當a>0時,函數y=f(x)在(
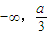
)上遞增,
在
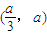
上遞減,在

上遞增,
故有
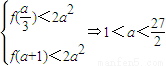
當a<0時,函數y=f(x)在
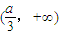
上遞增,
∴只要f(1-a)<2a
2⇒4a
3-6a
2+5a-1>0
令g(a)=4a
3-6a
2+5a-1,
則
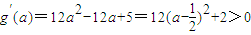
所以g(a)在(-∞,0)上遞增,
又g(0)=-1<0∴f(1-a)<2a
2不能恒成立
故所求的a的取值范圍為
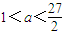 點評:
點評:本題考查已知函數的單調區間求參數范圍問題和不等式恒成立問題,體現分類討論和化歸思想.

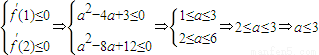
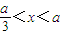 ,∴
,∴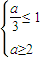 ∴2≤a≤3⇒a≤3
∴2≤a≤3⇒a≤3
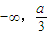 )上遞增,
)上遞增,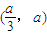 上遞減,在
上遞減,在 上遞增,
上遞增,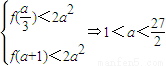
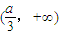 上遞增,
上遞增,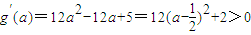
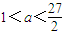


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案