
分析 (1)z是實數,則虛部等于0,求解即可得答案;
(2)z是純虛數,則實部等于0,虛部不等于0,求解即可得答案;
(3)由z對應的點在第四象限,列出不等式組,求解即可得答案.
解答 解:(1)復數z=(x2+x-2)+(x2-3x+2)i,
當z是實數時,x2-3x+2=0,解得x=1或x=2;
(2)當z是純虛數時,$\left\{\begin{array}{l}{x^2}+x-2=0\\{x^2}-3x+2≠0\end{array}\right.$,解得x=-2;
(3)當對應的點在第四象限時,則$\left\{\begin{array}{l}{{x}^{2}+x-2>0}\\{{x}^{2}-3x+2<0}\end{array}\right.$,解得1<x<2,
∴x的取值范圍為1<x<2.
點評 本題考查了復數的基本概念,考查了復數的代數表示法及其幾何意義,是基礎題.


科目:高中數學 來源: 題型:解答題
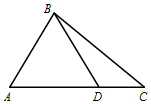 在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.
在△ABC中(圖),$A=\frac{π}{3},cosC=\frac{{2\sqrt{7}}}{7},BC=\sqrt{7},\overrightarrow{AD}=2\overrightarrow{DC}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com