
已知函數f(x)=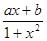 是定義在(-1,1)上的奇函數,且f(
是定義在(-1,1)上的奇函數,且f(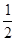 )=
)=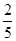 .
.
(1)試確定函數f(x)的解析式;(2)用定義證明f(x)在(-1,1)上是增函數;(3)解不等式f(t-1)+f(t)<0.
(1)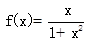 (2)見解析 (3)
(2)見解析 (3) 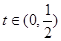 。
。
【解析】R上的奇函數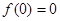 ,利用這點可以求某一參數;求單調性可以用定義或導數,判定自變量的大小與函數值的大小的關系;解具有單調性的函數不等式時,可以利用增函數的定義,函數值大的自變量大來解。
,利用這點可以求某一參數;求單調性可以用定義或導數,判定自變量的大小與函數值的大小的關系;解具有單調性的函數不等式時,可以利用增函數的定義,函數值大的自變量大來解。
已知函數f(x)=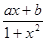 是定義在(-1,1)上的奇函數,
是定義在(-1,1)上的奇函數,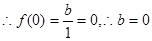 ,
,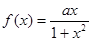 且f(
且f(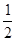 )=
)=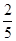 ,代入得
,代入得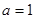 ,
,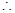
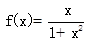
(2)任取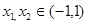 ,且
,且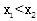 則
則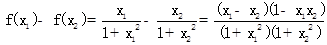
由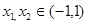 得
得 >0,由
>0,由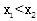 得
得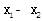 <0,所以
<0,所以 <0,即
<0,即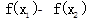 <0,即
<0,即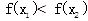 ,所以f(x)在(-1,1)上是增函數.
,所以f(x)在(-1,1)上是增函數.
(3) 由f(t-1)+f(t)<0得f (t) < — f(t-1);又f(x)是奇函數,故f (t) < f(1-t);因為f(x)在(-1,1)上是增函數,所以—1 <
t<1-t<1,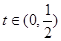


 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:高中數學 來源:2015屆山東省高一10月月考數學試卷(解析版) 題型:解答題
已知函數f(x)= 是奇函數.
是奇函數.
(1)求實數m的值;
(2)若函數f(x)在區間[-1,a-2]上單調遞增,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012年人教A版高中數學必修1單調性與最大(小)值練習卷(二)(解析版) 題型:選擇題
(2009廣西北海一檢,文10)已知函數f(x)= 是(-∞,+∞)上的減函數,那么a的取值范圍是( )
是(-∞,+∞)上的減函數,那么a的取值范圍是( )
A.(0,3) B.(0,3]
C.(0,2) D.(0,2]
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省漳州市三校高三第二次聯考文科數學 題型:選擇題
已知函數f(x+1)是定義在R上的奇函數,若對于任意給定的不等實數x1、x2,不等式 恒成立,則不等式f(1-x)<0的解集為(
)
恒成立,則不等式f(1-x)<0的解集為(
)
A.(1,+∞) B.(0,+∞) C.(-∞,0) D.(-∞,1)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江蘇省高三下學期開學質量檢測數學試卷 題型:解答題
(本小題滿分16分)已知函數f(x)= 是定義在R上的奇函數,其值域為
是定義在R上的奇函數,其值域為 .
.
(1) 試求a、b的值;
(2) 函數y=g(x)(x∈R)滿足:
條件1: 當x∈[0,3)時,g(x)=f(x);條件2: g(x+3)=g(x)lnm(m≠1).
① 求函數g(x)在x∈[3,9)上的解析式;
② 若函數g(x)在x∈[0,+∞)上的值域是閉區間,試探求m的取值范圍,并說明理由.
查看答案和解析>>
科目:高中數學 來源:2012屆度遼寧省沈陽市高三數學質量檢測試卷 題型:解答題
已知函數f(x)= 是定義在(-1,1)上的奇函數,且f(
是定義在(-1,1)上的奇函數,且f( )=
)= .
.
(1)求函數f(x)的解析式;
(2)用定義證明f(x)在(-1,1)上是增函數;
(3)解不等式f(t-1)+f(t)<0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com