
| A. | 16π | B. | 8π | C. | 4π | D. | 2π |
分析 由已知中$\overrightarrow{AB}$•$\overrightarrow{AD}$=${\overrightarrow{AB}}^{2}$,可得AB⊥BD,沿BD折起后,由平面ABD⊥平面BDC,可得三棱錐A-BCD的外接球的直徑為AC,進而根據2${\overrightarrow{AB}}^{2}$=4-${\overrightarrow{BD}}^{2}$,求出三棱錐A-BCD的外接球的半徑,可得三棱錐A-BCD的外接球的表面積.
解答 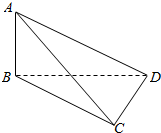 解:平行四邊形ABCD中,
解:平行四邊形ABCD中,
∵$\overrightarrow{AB}$•$\overrightarrow{AD}$=${\overrightarrow{AB}}^{2}$,
∴$\overrightarrow{AB}•\overrightarrow{BD}$=0,
∴AB⊥BD,
沿BD折成直二面角A-BD-C,
∵平面ABD⊥平面BDC
三棱錐A-BCD的外接球的直徑為AC,
∴AC2=AB2+BD2+CD2=2AB2+BD2=4
∴外接球的半徑為1,
故表面積是4π.
故選C.
點評 本題考查的知識點是球內接多面體,平面向量數量積的運算,其中根據已知求出三棱錐A-BCD的外接球的半徑是解答的關鍵.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
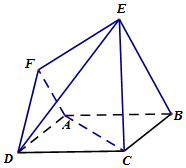 在如圖所示的六面體中,面ABCD是邊長為2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.
在如圖所示的六面體中,面ABCD是邊長為2的正方形,面ABEF是直角梯形,∠FAB=90°,AF∥BE,BE=2AF=4.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{1}{3}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (1,8) | D. | (8,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 橢圓$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的兩頂點為A,B如圖,離心率為$\frac{{\sqrt{2}}}{2}$,過其焦點F(0,1)的直線l與橢圓交于C,D兩點,并與x軸交于點P,直線AC與直線BD交于點Q.
橢圓$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1({a>b>0})$的兩頂點為A,B如圖,離心率為$\frac{{\sqrt{2}}}{2}$,過其焦點F(0,1)的直線l與橢圓交于C,D兩點,并與x軸交于點P,直線AC與直線BD交于點Q.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com