【答案】
分析:不妨設a≥b≥c>0,則lga≥lgb≥lgc,據排序不等式,可得三個不等式,相加,即可得出結論.
解答:證明:不妨設a≥b≥c>0,則lga≥lgb≥lgc.
據排序不等式有:
alga+blgb+clgc≥blga+clgb+algc
alga+blgb+clgc≥clga+algb+blgc
alga+blgb+clgc=alga+blgb+clgc
上述三式相加得:
3(alga+blgb+clgc)≥(a+b+c)(lga+lgb+lgc)
即lg(a
ab
bc
c)≥
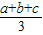
lg(abc)
故a
ab
bc
c≥(abc)
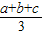
.
點評:本題考查不等式的證明,考查排序不等式,考查學生分析解決問題的能力,屬于中檔題.

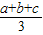 .
.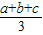 lg(abc)
lg(abc)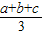 .
.

 閱讀快車系列答案
閱讀快車系列答案