
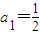 ,an+1-an=
,an+1-an= (n∈N*).
(n∈N*).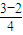 >0,可知a2>a1,當n≥2時,an+1-an=
>0,可知a2>a1,當n≥2時,an+1-an=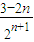 <0,可得an+1<an.因此當n≥2時,數列{an}是遞減數列,因而可知數列{an}中最大項為a2.
<0,可得an+1<an.因此當n≥2時,數列{an}是遞減數列,因而可知數列{an}中最大項為a2.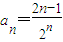 ;再檢查當n=1時,通項式是否符合,若不符合,則分情況,若符合,則該數列的通項公式為
;再檢查當n=1時,通項式是否符合,若不符合,則分情況,若符合,則該數列的通項公式為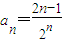 .
.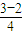 >0.
>0.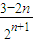 <0,
<0,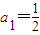 ,an+1-an=
,an+1-an=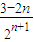 (n∈N*),
(n∈N*),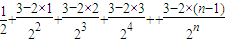 ,①
,①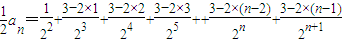 ,②
,②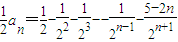 ,
,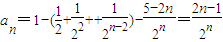 .
. 適合上式,
適合上式,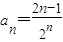 (n∈N*).
(n∈N*).

 三點一測快樂周計劃系列答案
三點一測快樂周計劃系列答案科目:高中數學 來源: 題型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com