
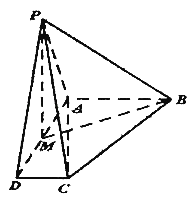
【題目】四棱錐P﹣ABCD中平面PAD⊥平面ABCD,AB∥CD,AB⊥AD,M為AD中點,PA=PD![]() ,AD=AB=2CD=2.
,AD=AB=2CD=2.
(1)求證:平面PMB⊥平面PAC;
(2)求二面角A﹣PC﹣D的余弦值.
【答案】(1)證明見詳解;(2)![]()
【解析】
(1)由直線![]() 垂直于
垂直于![]() ,可得線面垂直,再由線面垂直推證面面垂直即可;
,可得線面垂直,再由線面垂直推證面面垂直即可;
(2)以![]() 為坐標(biāo)原點,建立空間直角坐標(biāo)系,通過求解兩平面法向量的夾角,從而求得對應(yīng)二面角的余弦值.
為坐標(biāo)原點,建立空間直角坐標(biāo)系,通過求解兩平面法向量的夾角,從而求得對應(yīng)二面角的余弦值.
(1)證明:∵PA=PD,M為AD中點,
∴PM⊥AD,
又平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PM⊥平面ABCD,
又因為![]() 平面
平面![]() ,
,
故![]() .
.
由已知可得,tan![]() ,
,
∴∠ABM=∠DAC,
又∵![]() ,
,
∴![]() ,
,
∴MB⊥AC,
又![]() 平面
平面![]() ,
,
故可得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]()
∴平面PMB⊥平面PAC,即證.
(2)以M為坐標(biāo)原點,分別以MD,MP為x軸與z軸,
建立空間直角坐標(biāo)系,如下圖所示:
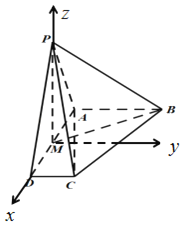
則A(﹣1,0,0),D(1,0,0),C(1,1,0),P(0,0,2).
設(shè)平面PAC的一個法向量為![]() .
.
![]() .
.
由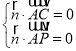 ,可得
,可得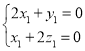 ,
,
令z1=1,得![]()
![]() ;
;
設(shè)平面PDC的一個法向量![]() ,
,
![]()
由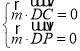 ,可得
,可得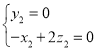 ,
,
取z2=1,得![]()
![]() .
.
設(shè)所求二面角為θ,又![]() 為銳二面角,
為銳二面角,
故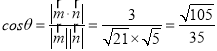 .
.
二面角A﹣PC﹣D的余弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 為矩形,
為矩形,![]() ,
,![]() 均為等邊三角形,
均為等邊三角形,![]() ,
,![]() .
.
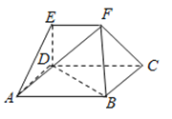
(Ⅰ)過![]() 作截面與線段
作截面與線段![]() 交于點
交于點![]() ,使得
,使得![]() 平面
平面![]() ,試確定點
,試確定點![]() 的位置,并予以證明;
的位置,并予以證明;
(Ⅱ)在(Ⅰ)的條件下,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,滿足acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若△ABC的周長為3,求△ABC的內(nèi)切圓面積S的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了慶祝中華人民共和國成立![]() 周年,某車間內(nèi)舉行生產(chǎn)比賽,由甲乙兩組內(nèi)各隨機選取
周年,某車間內(nèi)舉行生產(chǎn)比賽,由甲乙兩組內(nèi)各隨機選取![]() 名技工,在單位時間生產(chǎn)同一種零件,其生產(chǎn)的合格零件數(shù)的莖葉圖如下:
名技工,在單位時間生產(chǎn)同一種零件,其生產(chǎn)的合格零件數(shù)的莖葉圖如下:
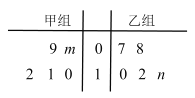
已知兩組所選技工生產(chǎn)的合格零件的平均數(shù)均為![]() .
.
(1)分別求出![]() 的值;
的值;
(2)分別求出甲乙兩組技工在單位時間內(nèi)加工的合格零件的方差![]() 和
和![]() ,并由此估計兩組技工的生產(chǎn)水平;
,并由此估計兩組技工的生產(chǎn)水平;
(3)若單位時間內(nèi)生產(chǎn)的合格零件個數(shù)不小于平均數(shù)的技工即為“生產(chǎn)能手”,根據(jù)以上數(shù)據(jù),能否認(rèn)為該車間50%以上的技工都是生產(chǎn)能手?
(注:方差![]() ,其中
,其中![]() 為數(shù)據(jù)
為數(shù)據(jù)![]() 的平均數(shù)).
的平均數(shù)).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)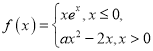
①當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有______零點;
有______零點;
②若函數(shù)![]() 的值域為
的值域為![]() ,則實數(shù)
,則實數(shù)![]() 的取值范圍是______.
的取值范圍是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() ,
,![]() 為自然對數(shù)的底數(shù).
為自然對數(shù)的底數(shù).
(1)當(dāng)![]() 時,判斷
時,判斷![]() 零點個數(shù)并求出零點;
零點個數(shù)并求出零點;
(2)若函數(shù)![]() 存在兩個不同的極值點
存在兩個不同的極值點![]() ,
,![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AB//CD,∠ABC=![]() ,BC=CD=CE=1,EC⊥平面ABCD,EF
,BC=CD=CE=1,EC⊥平面ABCD,EF![]() AC,P是線段EF上的動點
AC,P是線段EF上的動點
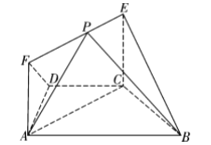
(1)求證:平面BCE⊥平面ACEF;
(2)求平面PAB與平面BCE所成銳二面角![]() 的最小值
的最小值
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=ax+x2,g(x)=xlna,a>1.
(1)求證:函數(shù)F(x)=f(x)-g(x)在(0,+∞)上單調(diào)遞增;
(2)若函數(shù)y=![]() -3有四個零點,求b的取值范圍;
-3有四個零點,求b的取值范圍;
(3)若對于任意的x1,x2∈[-1,1]時,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在極坐標(biāo)系中,直線的方程為2ρcosθ+5ρsinθ﹣8=0,曲線E的方程為ρ=4cosθ.
(1)以極點O為直角坐標(biāo)原點,極軸為x軸正半軸建立平面直角坐標(biāo)系,分別寫出直線l與曲線E的直角坐標(biāo)方程;
(2)設(shè)直線l與曲線E交于A,B兩點,點C在曲線E上,求△ABC面積的最大值,并求此時點C的直角坐標(biāo).
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com