Question

函數f(x)=log2x-3sin(

π

2

x)零點的個數是（　　）

A．2

B．3

C．4

D．5

Answer 1

分析：函數f(x)=log2x-3sin(

π

2

x)的零點即log2x-3sin(

π

2

x)=0的根，設h（x）=3sin（

π

2

x），g（x）=log₂x，在同一坐標系內作出g（x）和h（x）的圖象，通過討論h（x、g（x）的單調性與最值，得它們有且僅有3個交點，由此可得原函數零點的個數．

解答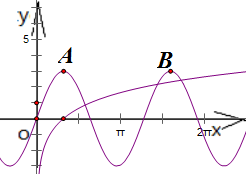：解：函數f(x)=log2x-3sin(

π

2

x)的零點即
方程log2x-3sin(

π

2

x)=0的根，由此可得
設h（x）=3sin（

π

2

x），g（x）=log₂x，
在同一坐標系內作出g（x）和h（x）的圖象
函數g（x）=log₂x是對數函數，因為2＞1，所以圖象為經過點（1，0）的增函數的曲線
而h（x）=3sin（

π

2

x）的周期為T=

2π

π 2

=4，在原點的右側它的第一個最大值點為x=1，對應圖中A（1，3），第二個最大值點為x=5，對應圖中B（5，3）
∵log₂5＜3，
∴曲線g（x）=log₂x經過點B的下方，在B的左右各有一個交點
當x≤8時，log₂x≤3，兩個函數圖象有3個交點；
而當x＞8時，h（x）=3sin（

π

2

x）≤3＜g（x）=log₂x，兩圖象不可能有交點
∴h（x）=3sin（

π

2

x）與g（x）=log₂x的圖象有且僅有3個不同的交點，得函數f(x)=log2x-3sin(

π

2

x)的零點有3個
故答案為：B

點評：本題給出含有三角函數和對數的函數，求函數的零點的個數，著重考查了基本初等函數的單調性、最值和函數零點的求法等知識，屬于中檔題．