
 如圖,等腰直角△ABC中,AB=AC=1,在邊AB、AC上分別取D、E兩點(diǎn),沿線段DE折疊,頂點(diǎn)A恰好落在邊BC上,則AD長(zhǎng)度的最小值為$\sqrt{2}$-1..
如圖,等腰直角△ABC中,AB=AC=1,在邊AB、AC上分別取D、E兩點(diǎn),沿線段DE折疊,頂點(diǎn)A恰好落在邊BC上,則AD長(zhǎng)度的最小值為$\sqrt{2}$-1.. 分析 如圖,連接AA′,設(shè)∠BDA′=θ∈$(0,\frac{3π}{4})$.可設(shè)AD=DP=x,AB=1,則BD=1-x.在△BDA′中,由正弦定理有:$\frac{BD}{sin∠B{A}^{′}D}$=$\frac{1-x}{sin(\frac{3π}{4}-θ)}$=$\frac{x}{sinB}$=$\sqrt{2}$x.可得:x=$\frac{1}{\sqrt{2}sin(\frac{3π}{4}-θ)+1}$.即可得出.
解答 解:如圖,連接AA′,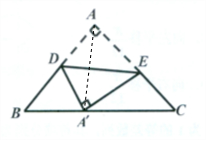 設(shè)∠BDA′=θ∈$(0,\frac{3π}{4})$.
設(shè)∠BDA′=θ∈$(0,\frac{3π}{4})$.
由AD=DA′,
可設(shè)AD=DP=x,AB=1,則BD=1-x
在△BDA′中,由正弦定理有:$\frac{BD}{sin∠B{A}^{′}D}$=$\frac{1-x}{sin(\frac{3π}{4}-θ)}$=
$\frac{x}{sinB}$=$\frac{x}{sin\frac{π}{4}}$=$\sqrt{2}$x.
可得:x=$\frac{1}{\sqrt{2}sin(\frac{3π}{4}-θ)+1}$.
∴當(dāng)θ=$\frac{π}{4}$時(shí),x取得最小值,x=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1.
故答案為:$\sqrt{2}$-1.
點(diǎn)評(píng) 本題考查了正弦定理、三角函數(shù)的單調(diào)性與值域,考查了推理能力與計(jì)算能力,屬于中檔題.


 單元期中期末卷系列答案
單元期中期末卷系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3-$\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3+$\sqrt{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2個(gè) | B. | 4個(gè) | C. | 8個(gè) | D. | 無窮個(gè) |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com