
【題目】已知函數f(x)= ![]() ,直線y=
,直線y= ![]() x(a≠0)為曲線y=f(x)的一條切線.
x(a≠0)為曲線y=f(x)的一條切線.
(1)求實數a的值;
(2)用min{m,n}表示m,n中的最小值,設函數g(x)=min{f(x),x﹣ ![]() }(x>0),若函數h(x)=g(x)﹣bx2為增函數,求實數b的取值范圍.
}(x>0),若函數h(x)=g(x)﹣bx2為增函數,求實數b的取值范圍.
【答案】
(1)解:設切點坐標為(x0,y0),f′(x)= ![]() ,則
,則  ,∴a=1;
,∴a=1;
(2)解:記F(x)=f(x)﹣(x﹣ ![]() ),x>0.下面考察y=F(x)的符號.
),x>0.下面考察y=F(x)的符號.
求導F′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() ,
,
x≥2,F′(x)<0,0<x<2,x(2﹣x)≤1,∴F′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() ≤﹣
≤﹣ ![]() <0,
<0,
∴F(x)在(0,+∞)上單調遞減,
∵F(1)= ![]() >0,F(2)=
>0,F(2)= ![]() ﹣
﹣ ![]() <0,
<0,
∴F(x)在[1,2]上有唯一零點x0,
∴g(x)= 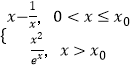 ,
,
∴h(x)=g(x)﹣bx2= 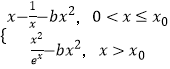 ,
,
x>x0,h′(x)= ![]() ﹣2bx≥0恒成立,∴2b≤
﹣2bx≥0恒成立,∴2b≤ ![]() ,
,
設u(x)= ![]() ,u′(x)=
,u′(x)= ![]() ,函數在(x0,3)上單調遞減,(3,+∞)上單調遞增,
,函數在(x0,3)上單調遞減,(3,+∞)上單調遞增,
∴u(x)min=﹣ ![]() ,∴2b≤﹣
,∴2b≤﹣ ![]() ,∴b≤﹣
,∴b≤﹣ ![]() ;
;
0<x≤x0時,h′(x)=1+ ![]() ﹣2bx,b≤0,h′(x)>0在(0,x0)上恒成立,
﹣2bx,b≤0,h′(x)>0在(0,x0)上恒成立,
綜上所述,b≤﹣ ![]() 時,函數h(x)=g(x)﹣bx2為增函數.
時,函數h(x)=g(x)﹣bx2為增函數.
【解析】(1)根據直線y= ![]() x(a≠0)為曲線y=f(x)的一條切線,求實數a的值;(2)記F(x)=f(x)﹣(x﹣
x(a≠0)為曲線y=f(x)的一條切線,求實數a的值;(2)記F(x)=f(x)﹣(x﹣ ![]() ),x>0.考察y=F(x)的符號,得出g(x)=
),x>0.考察y=F(x)的符號,得出g(x)= 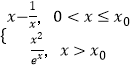 ,再分類討論,利用導數的正負,即可得出結論.
,再分類討論,利用導數的正負,即可得出結論.
【考點精析】掌握利用導數研究函數的單調性是解答本題的根本,需要知道一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減.
在這個區間單調遞減.


 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案 激活思維優加課堂系列答案
激活思維優加課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,直線PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4. 
(1)求證:直線DE⊥平面PAC.
(2)若直線PE與平面PAC所成的角的正弦值為 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,0),若函數f(x)的圖象上存在兩點B、C到點A的距離相等,則稱該函數f(x)為“點距函數”,給定下列三個函數:①y=﹣x+2;② ![]() ;③y=x+1.其中,“點距函數”的個數是( )
;③y=x+1.其中,“點距函數”的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,D為BC的中點,∠BAD+∠C≥90°. (Ⅰ)求證:sin2C≤sin2B;
(Ⅱ)若cos∠BAD=﹣ ![]() ,AB=2,AD=3,求AC.
,AB=2,AD=3,求AC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】17世紀日本數學家們對這個數學關于體積方法的問題還不了解,他們將體積公式“V=kD3”中的常數k稱為“立圓術”或“玉積率”,創用了求“玉積率”的獨特方法“會玉術”,其中,D為直徑,類似地,對于等邊圓柱(軸截面是正方形的圓柱叫做等邊圓柱)、正方體也有類似的體積公式V=kD3 , 其中,在等邊圓柱中,D表示底面圓的直徑;在正方體中,D表示棱長,假設運用此“會玉術”,求得的球、等邊圓柱、正方體的“玉積率”分別為k1 , k2 , k3=( )
A.![]() :
: ![]() :1
:1
B.![]() :
: ![]() :2
:2
C.1:3: ![]()
D.1: ![]() :
: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC= ![]() ,點E在AD上,且AE=2ED. (Ⅰ)已知點F在BC上,且CF=2FB,求證:平面PEF⊥平面PAC;
,點E在AD上,且AE=2ED. (Ⅰ)已知點F在BC上,且CF=2FB,求證:平面PEF⊥平面PAC;
(Ⅱ)當二面角A﹣PB﹣E的余弦值為多少時,直線PC與平面PAB所成的角為45°?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}的前n(n∈N*)項和為Sn , a3=3,且λSn=anan+1 , 在等比數列{bn}中,b1=2λ,b3=a15+1. (Ⅰ)求數列{an}及{bn}的通項公式;
(Ⅱ)設數列{cn}的前n(n∈N*)項和為Tn , 且 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com