
已知函數
 滿足
滿足 ,對于任意
,對于任意 R都有
R都有 ,且
,且  ,令
,令 .
.
(Ⅰ)求函數 的表達式;
的表達式;
(Ⅱ)求函數 的單調區間;
的單調區間;
(Ⅲ)研究函數 在區間
在區間 上的零點個數.
上的零點個數.
∵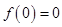 ,∴
,∴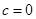 .
…… 1分
.
…… 1分
∵對于任意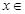 R都有
R都有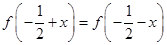 ,
,
∴函數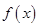 的對稱軸為
的對稱軸為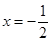 ,即
,即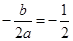 ,得
,得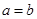 . …… 2分
. …… 2分
又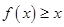 ,即
,即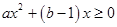 對于任意
對于任意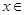 R都成立,
R都成立,
∴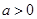 ,且
,且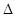
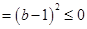 .
.
∵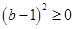 , ∴
, ∴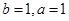 .
.
∴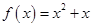 .
…… 4分
.
…… 4分
(2) 解: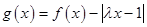
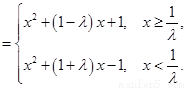 …… 5分
…… 5分
① 當 時,函數
時,函數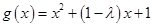 的對稱軸為
的對稱軸為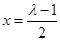 ,
,
若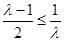 ,即
,即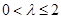 ,函數
,函數 在
在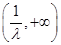 上單調遞增; …… 6分
上單調遞增; …… 6分
若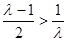 ,即
,即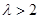 ,函數
,函數 在
在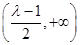 上單調遞增,在
上單調遞增,在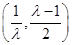 上單調遞減. …… 7分
上單調遞減. …… 7分
② 當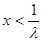 時,函數
時,函數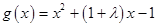 的對稱軸為
的對稱軸為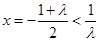 ,
,
則函數 在
在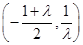 上單調遞增,在
上單調遞增,在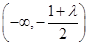 上單調遞減. …… 8分
上單調遞減. …… 8分
綜上所述,當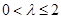 時,函數
時,函數 單調遞增區間為
單調遞增區間為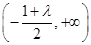 ,單調遞減區間為
,單調遞減區間為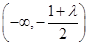 ;
…… 9分
;
…… 9分
當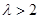 時,函數
時,函數 單調遞增區間為
單調遞增區間為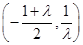 和
和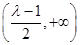 ,單調遞減區間為
,單調遞減區間為
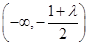 和
和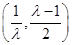 .
…… 10分
.
…… 10分
(3)解:①
當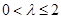 時,由(2)知函數
時,由(2)知函數 在區間
在區間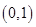 上單調遞增,
上單調遞增,
又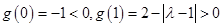 ,
,
故函數 在區間
在區間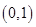 上只有一個零點. …… 11分
上只有一個零點. …… 11分
② 當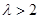 時,則
時,則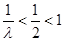 ,而
,而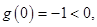
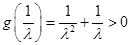 ,
,
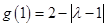 ,
,
(ⅰ)若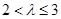 ,由于
,由于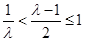 ,
,
且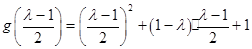
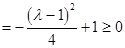 ,
,
此時,函數 在區間
在區間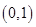 上只有一個零點;
…… 12分
上只有一個零點;
…… 12分
(ⅱ)若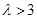 ,由于
,由于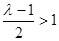 且
且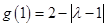
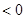 ,此時,函數
,此時,函數 在區間
在區間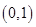 上有兩個不同的零點.
…… 13分
上有兩個不同的零點.
…… 13分
綜上所述,當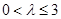 時,函數
時,函數 在區間
在區間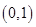 上只有一個零點;
上只有一個零點;
當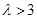 時,函數
時,函數 在區間
在區間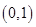 上有兩個不同的零點.
上有兩個不同的零點.
【解析】略


科目:高中數學 來源: 題型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2+2x+n |
查看答案和解析>>
科目:高中數學 來源:2012屆上海市高三第一學期期中理科數學試卷 題型:解答題
若定義在 上的函數
上的函數 滿足條件:存在實數
滿足條件:存在實數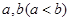 且
且

 ,使得:
,使得:
⑴ 任取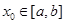 ,有
,有 (
( 是常數);
是常數);
⑵ 對于 內任意
內任意 ,當
,當 ,總有
,總有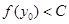 。
。
我們將滿足上述兩條件的函數 稱為“平頂型”函數,稱
稱為“平頂型”函數,稱 為“平頂高度”,稱
為“平頂高度”,稱 為“平頂寬度”。根據上述定義,解決下列問題:
為“平頂寬度”。根據上述定義,解決下列問題:
(1)函數 是否為“平頂型”函數?若是,求出“平頂高度”和“平頂寬度”;若不是,簡要說明理由。
是否為“平頂型”函數?若是,求出“平頂高度”和“平頂寬度”;若不是,簡要說明理由。
(2) 已知 是“平頂型”函數,求出
是“平頂型”函數,求出 的值。
的值。
(3)對于(2)中的函數 ,若
,若 在
在 上有兩個不相等的根,求實數
上有兩個不相等的根,求實數 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源:2010年高考試題(上海秋季)解析版(理) 題型:解答題
[番茄花園1] 本題共有3個小題,第1小題滿分3分,第2小題滿分5分,第3小題滿分10分。
若實數 、
、 、
、 滿足
滿足 ,則稱
,則稱 比
比 遠離
遠離 .
.
(1)若 比1遠離0,求
比1遠離0,求 的取值范圍;
的取值范圍;
(2)對任意兩個不相等的正數 、
、 ,證明:
,證明: 比
比 遠離
遠離 ;
;
(3)已知函數 的定義域
的定義域 .任取
.任取 ,
, 等于
等于 和
和 中遠離0的那個值.寫出函數
中遠離0的那個值.寫出函數 的解析式,并指出它的基本性質(結論不要求證明).
的解析式,并指出它的基本性質(結論不要求證明).
23本題共有3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
已知橢圓 的方程為
的方程為 ,點P的坐標為(-a,b).
,點P的坐標為(-a,b).
(1)若直角坐標平面上的點M、A(0,-b),B(a,0)滿足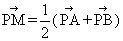 ,求點
,求點 的坐標;
的坐標;
(2)設直線 交橢圓
交橢圓 于
于 、
、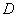 兩點,交直線
兩點,交直線 于點
于點 .若
.若 ,證明:
,證明: 為
為 的中點;
的中點;
(3)對于橢圓 上的點Q(a cosθ,b sinθ)(0<θ<π),如果橢圓
上的點Q(a cosθ,b sinθ)(0<θ<π),如果橢圓 上存在不同的兩個交點
上存在不同的兩個交點 、
、 滿足
滿足 ,寫出求作點
,寫出求作點 、
、 的步驟,并求出使
的步驟,并求出使 、
、 存在的θ的取值范圍.
存在的θ的取值范圍.
[番茄花園1]22.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年黑龍江省大慶市鐵人中學高三(上)第二次段考數學試卷(解析版) 題型:選擇題
 ,3},則使函數y=xa的定義域為R且該函數為奇函數的所有a的值為1,3;
,3},則使函數y=xa的定義域為R且該函數為奇函數的所有a的值為1,3;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com