
[番茄花園1] 本題共有3個小題,第1小題滿分3分,第2小題滿分5分,第3小題滿分10分。
若實數 、
、 、
、 滿足
滿足 ,則稱
,則稱 比
比 遠離
遠離 .
.
(1)若 比1遠離0,求
比1遠離0,求 的取值范圍;
的取值范圍;
(2)對任意兩個不相等的正數 、
、 ,證明:
,證明: 比
比 遠離
遠離 ;
;
(3)已知函數 的定義域
的定義域 .任取
.任取 ,
, 等于
等于 和
和 中遠離0的那個值.寫出函數
中遠離0的那個值.寫出函數 的解析式,并指出它的基本性質(結論不要求證明).
的解析式,并指出它的基本性質(結論不要求證明).
23本題共有3個小題,第1小題滿分3分,第2小題滿分6分,第3小題滿分9分.
已知橢圓 的方程為
的方程為 ,點P的坐標為(-a,b).
,點P的坐標為(-a,b).
(1)若直角坐標平面上的點M、A(0,-b),B(a,0)滿足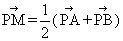 ,求點
,求點 的坐標;
的坐標;
(2)設直線 交橢圓
交橢圓 于
于 、
、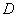 兩點,交直線
兩點,交直線 于點
于點 .若
.若 ,證明:
,證明: 為
為 的中點;
的中點;
(3)對于橢圓 上的點Q(a cosθ,b sinθ)(0<θ<π),如果橢圓
上的點Q(a cosθ,b sinθ)(0<θ<π),如果橢圓 上存在不同的兩個交點
上存在不同的兩個交點 、
、 滿足
滿足 ,寫出求作點
,寫出求作點 、
、 的步驟,并求出使
的步驟,并求出使 、
、 存在的θ的取值范圍.
存在的θ的取值范圍.
[番茄花園1]22.
[番茄花園1] 解析:(1) 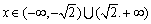 ;
;
(2) 對任意兩個不相等的正數a、b,有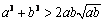 ,
,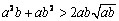 ,
,
因為 ,
,
所以 ,即a3+b3比a2b+ab2遠離
,即a3+b3比a2b+ab2遠離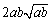 ;
;
(3)  ,
,
性質:1°f(x)是偶函數,圖像關于y軸對稱,2°f(x)是周期函數,最小正周期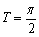 ,
,
3°函數f(x)在區間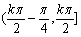 單調遞增,在區間
單調遞增,在區間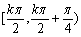 單調遞減,kÎZ,
單調遞減,kÎZ,
4°函數f(x)的值域為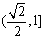 .
.
23解析:(1)  ;
;
(2) 由方程組 ,消y得方程
,消y得方程 ,
,
因為直線 交橢圓
交橢圓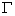 于
于 、
、 兩點,
兩點,
所以D>0,即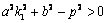 ,
,
設C(x1,y1)、D(x2,y2),CD中點坐標為(x0,y0),
則 ,
,
由方程組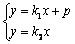 ,消y得方程(k2-k1)x=p,
,消y得方程(k2-k1)x=p,
又因為 ,所以
,所以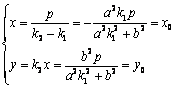 ,
,
故E為CD的中點;
(3) 求作點P1、P2的步驟:1°求出PQ的中點 ,
,
2°求出直線OE的斜率 ,
,
3°由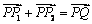 知E為CD的中點,根據(2)可得CD的斜率
知E為CD的中點,根據(2)可得CD的斜率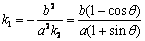 ,
,
4°從而得直線CD的方程: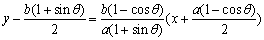 ,
,
5°將直線CD與橢圓Γ的方程聯立,方程組的解即為點P1、P2的坐標.
欲使P1、P2存在,必須點E在橢圓內,
所以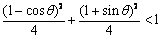 ,化簡得
,化簡得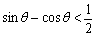 ,
,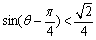 ,
,
又0<q <p,即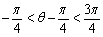 ,所以
,所以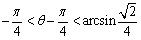 ,
,
故q 的取值范圍是 .
.
[番茄花園1]22.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com