【題目】函數
.
（1）討論
在
上的最大值；
（2）有幾個
（
，且為常數），使得函數
在
上的最大值為
？
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某企業接到生產3000臺某產品的
三種部件的訂單，每臺產品需要這三種部件的數量分別為2,2,1（單位：件）,已知每個工人每天可生產A部件6件，或B部件3件，或C部件2件.該企業計劃安排200名工人分成三組分別生產這三種部件，生產B部件的人數與生產A部件的人數成正比，比例系數為k（k為正整數）.
（1）設生產
部件的人數為
，分別寫出完成三種部件生產需要的時間；
（2）假設這三種部件的生產同時開工，試確定正整數k的值，使完成訂單任務的時間最短，并給出時間最短時具體的人數分組方案.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校高三男生體育課上做投籃球游戲，兩人一組，每輪游戲中，每小組兩人每人投籃兩次，投籃投進的次數之和不少于
次稱為“優秀小組”.小明與小亮同一小組，小明、小亮投籃投進的概率分別為
.
（1）若
，
，則在第一輪游戲他們獲“優秀小組”的概率；
（2）若
則游戲中小明小亮小組要想獲得“優秀小組”次數為
次，則理論上至少要進行多少輪游戲才行？并求此時的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
的焦點為
，準線為
，過的直線與
相交于
兩點.
（1）以
為直徑的圓與
軸交
兩點，若
，求
；
（2）點
在上，過點且垂直于
軸的直線與
分別相交于
兩點，證明：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
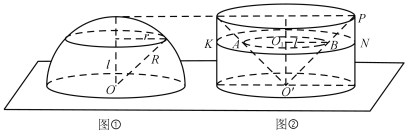
【題目】祖暅原理指出：兩個等高的幾何體若在所有等高處的水平截面的面積相等，則這兩個幾何體的體積相等，例如在計算球的體積時，構造一個底面半徑和高都與球的半徑相等的圓柱，與半球（如圖①）放置在同一平面上，然后在圓柱內挖去一個以圓柱下底面圓心為頂點，圓柱上底面為底面的圓錐后得到一新幾何體（如圖②），用任何一個平行于底面的平面去截它們時，可證得所截得的兩個截面面積相等，由此可證明新幾何體與半球體積相等.現將橢圓
所圍成的平面圖形繞y軸旋轉一周后得一橄欖狀的幾何體，類比上述方法，運用祖暅原理可求得其體積等于（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
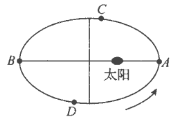
【題目】地球的公轉軌道可以看作是以太陽為一個焦點的橢圓，根據開普勒行星運動第二定律，可知太陽和地球的連線在相等的時間內掃過相等的面積，某同學結合物理和地理知識得到以下結論：①地球到太陽的距離取得最小值和最大值時，地球分別位于圖中
點和
點；②已知地球公轉軌道的長半軸長約為
千米，短半軸長約為
千米，則該橢圓的離心率約為
.因此該橢圓近似于圓形：③已知我國每逢春分（
月
日前后）和秋分（
月
日前后），地球會分別運行至圖中
點和
點，則由此可知我國每年的夏半年（春分至秋分）比冬半年（當年秋分至次年春分）要少幾天.以上結論正確的是（ ）
A.①B.①②C.②③D.①③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著社會經濟高速發展，人民的生活水平越來越高，部分學校安裝了中央空調，某校數學建模隊調查了某品牌中央空調，得到該設備使用年限x（單位：年）和維修總費用y（單位：萬元）的統計表如下：（每年年底維修保養）
使用年限x（單位：年） | 2 | 3 | 4 | 5 | 6 |
維修總費用y（單位：萬元） | 1 |
| 3 | 4 |
|
由上表可得線性回歸方程
，則根據此模型預報該品牌中央空調第8年年底的維修費用約為（ ）
A.
萬元B.
萬元C.
萬元D.
萬元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的中心在原點，左焦點
、右焦點
都在
軸上，點
是橢圓上的動點，
的面積的最大值為
，在軸上方使
成立的點只有一個．
（1）求橢圓的方程；
（2）過點
的兩直線
，
分別與橢圓交于點
，
和點
，
，且
，比較
與
的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
