
【題目】如圖,在直三棱柱![]() 中,點
中,點![]() 分別為線段
分別為線段![]() 的中點.
的中點.
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() 在邊
在邊![]() 上,
上,![]() ,求證:
,求證:![]() .
.
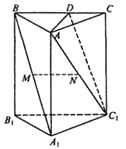
【答案】(1)詳見解析(2)詳見解析
【解析】試題分析:(1)由題意,利用三角形中位線定理可證MN∥BC,即可判定MN∥平面![]() ;(2)利用線面垂直的性質可證CC1⊥AD,結合已知可證AD⊥平面
;(2)利用線面垂直的性質可證CC1⊥AD,結合已知可證AD⊥平面![]() ,從而證明AD⊥BC,結合(1)知,MN∥BC,即可證明MN⊥AD
,從而證明AD⊥BC,結合(1)知,MN∥BC,即可證明MN⊥AD
試題解析:(1)如圖,連結A1C.]
在直三棱柱ABC-A1B1C1中,側面AA1C1C為平行四邊形.
又因為N為線段AC1的中點,
所以A1C與AC1相交于點N,
即A1C經過點N,且N為線段A1C的中點. ……………… 2分
因為M為線段A1B的中點,
所以MN∥BC. ……………… 4分
又MN平面BB1C1C,BC平面BB1C1C,
所以MN∥平面BB1C1C. ………………… 6分
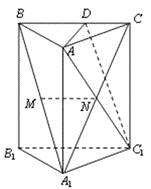
(2)在直三棱柱ABC-A1B1C1中,CC1⊥平面ABC.
又AD平面ABC,所以CC1⊥AD. …………………… 8分
因為AD⊥DC1,DC1平面BB1C1C,CC1平面BB1C1C,CC1∩DC1=C1,
所以AD⊥平面BB1C1C. …………………… 10分
又BC平面BB1C1C,所以AD⊥BC. …………………… 12分
又由(1)知,MN∥BC,所以MN⊥AD. …………………… 14分


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:
【題目】已知直線![]() 上有一個動點
上有一個動點![]() ,過點
,過點![]() 作直線
作直線![]() 垂直于
垂直于![]() 軸,動點
軸,動點![]() 在
在![]() 上,且滿足
上,且滿足![]() (
(![]() 為坐標原點),記點
為坐標原點),記點![]() 的軌跡為
的軌跡為![]() .
.
(I)求曲線![]() 的方程;
的方程;
(II)若直線![]() 是曲線
是曲線![]() 的一條切線,當點
的一條切線,當點![]() 到直線
到直線![]() 的距離最短時,求直線
的距離最短時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(A)已知平行四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() .
.
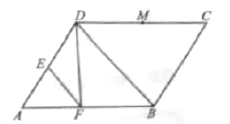
(1)求![]() 的長;
的長;
(2)設![]() ,
, ![]() 為線段
為線段![]() 、
、![]() 上的動點,且
上的動點,且![]() ,求
,求![]() 的最小值.
的最小值.
(B)已知平行四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() .
.
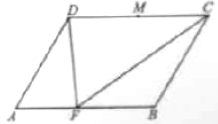
(1)求![]() 的長;
的長;
(2)設![]() 為線段
為線段![]() 上的動點(不包含端點),求
上的動點(不包含端點),求![]() 的最小值,以及此時點
的最小值,以及此時點![]() 的位置.
的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() :
:![]() ,點
,點![]() .
.
(1)過點![]() 的直線
的直線![]() 與圓交與
與圓交與![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)從圓![]() 外一點
外一點![]() 向該圓引一條切線,切點記為
向該圓引一條切線,切點記為![]() ,
,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,求使得
,求使得![]() 取得最小值時點
取得最小值時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 經過點
經過點![]() ,
,![]() ,且它的圓心在直線
,且它的圓心在直線![]() 上.
上.
(Ⅰ)求圓![]() 的方程;
的方程;
(Ⅱ)求圓![]() 關于直線
關于直線![]() 對稱的圓的方程。
對稱的圓的方程。
(Ⅲ)若點![]() 為圓
為圓![]() 上任意一點,且點
上任意一點,且點![]() ,求線段
,求線段![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王于年初用50萬元購買一輛大貨車,第一年因繳納各種費用需支出6萬元,從第二年起,每年都比上一年增加支出2萬元,假定該車每年的運輸收入均為25萬元.小王在該車運輸累計收入超過總支出后,考慮將大貨車作為二手車出售,若該車在第x年年底出售,其銷售價格為(25-x)萬元(國家規定大貨車的報廢年限為10年).
(1)大貨車運輸到第幾年年底,該車運輸累計收入超過總支出?
(2)在第幾年年底將大貨車出售,能使小王獲得的年平均利潤最大?(利潤=累計收入+銷售收入-總支出)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經過長期觀測得到:在交通繁忙的時段內,某公路汽車的車流量![]() (千輛/
(千輛/ ![]() )與汽車的平均速度
)與汽車的平均速度![]() 之間的函數關系式為
之間的函數關系式為![]() .
.
(I)若要求在該段時間內車流量超過2千輛/ ![]() ,則汽車在平均速度應在什么范圍內?
,則汽車在平均速度應在什么范圍內?
(II)在該時段內,當汽車的平均速度![]() 為多少時,車流量最大?最大車流量為多少?
為多少時,車流量最大?最大車流量為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代內容極為豐富的數學名著,書中將底面為直角三角形的直棱柱稱為塹堵,將底面為矩形的棱臺稱為芻童.在如圖所示的塹堵![]() 與芻童
與芻童![]() 的組合體中
的組合體中![]() ,
,![]() .臺體體積公式:
.臺體體積公式:![]() ,其中
,其中![]() 分別為臺體上、下底面面積,
分別為臺體上、下底面面積,![]() 為臺體高.
為臺體高.
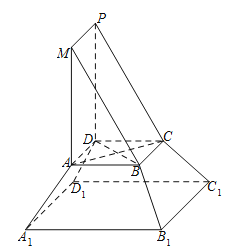
(Ⅰ)證明:直線![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,三棱錐
,三棱錐![]() 的體積
的體積![]() ,求該組合體的體積.
,求該組合體的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com