某電子原件生產廠生產的10件產品中,有8件一級品,2件二級品,一級品和二級品在外觀上沒有區別.從這10件產品中任意抽檢2件,計算:
(1)2件都是一級品的概率;
(2)至少有一件二級品的概率.
【答案】
分析:(1)本題是一個等可能事件的概率,從10件產品中抽取2件,共有C
102個基本事件,而滿足條件的事件的結果有C
82,根據等可能事件的概率公式得到結果.
(2)至少有一件二級品包括抽取的2件產品中包含了一件一級品,一件二級品與抽取的2件產品均為二級品,這兩種情況是互斥的,根據互斥事件的概率公式和等可能事件的概率公式得到結果.
解答:解:(1)由題意知本題是一個等可能事件的概率,
設2件都是一級品為事件A.…(1分)
從10件產品中抽取2件,共有C
102=45個基本事件,且都是等可能的(2分)
而事件A的結果有C
82=28種,…(4分)
則P(A)=

. …(5分)
(2)設至少有一件二級品為事件B,…(6分)
則B是兩個互斥事件:“抽取的2件產品中包含了一件一級品,
一件二級品(記為B
1)”與“抽取的2件產品均為二級品(B
2)”的和. …(7分)
而P(B
1)=

,P(B
2)=

,…(8分)
∴P(B)=P(B
1+B
2)=P(B
1)+P(B
2) …(10分)
=
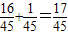
. …(11分)
答:2件都是一級品的概率為
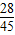
;至少有一件二級品的概率為
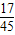
.(12分)
點評:本題考查等可能事件的概率和互斥事件的概率,本題解題的關鍵是看清楚要求的事件包含的事件數,熟練應用概率公式,本題是一個中檔題目.

 . …(5分)
. …(5分) ,P(B2)=
,P(B2)= ,…(8分)
,…(8分)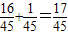 . …(11分)
. …(11分)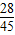 ;至少有一件二級品的概率為
;至少有一件二級品的概率為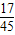 .(12分)
.(12分)
