已知函數f(x)=ex,g(x)=ax+1(a是不為零的常數,且a∈R).
(1)討論函數F(x)=f(x)•g(x)的單調性;
(2)當a=-1時,方程f(x)•g(x)=t在區間[-1,1]上有兩個解,求實數t的取值范圍.
解:(1)由題意可得F(x)=f(x)g(x)=e
x(ax+1)
∴F′(x)=e
x(ax+a+1)
令∴F′(x)=e
x(ax+a+1)=0
∴
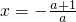
∴當a>0時F(x)=f(x)•g(x)的單調增區間為(

,+∞)單調減區間為(-∞,

)
當a<0時F(x)=f(x)•g(x)的單調增區間為(-∞,

)單調減區間為(

,+∞)
(2)由題意可得當a=-1時,F(x)=f(x)•g(x)=e
x(-x+1)
由(1)可得當a=-1時可以得出F(x)在(-∞,0)上為增函數,在(0,+∞)上為減函數
∴函數的最大值為F(0)=1
又∵方程f(x)•g(x)=t在區間[-1,1]上有兩個解
∴實數t的取值范圍是(-∞,1).
分析:(1)求函數F(x)=f(x)•g(x)的導數F′(x),再根據F′(x)的零點,討論實數a的取值,可得F′(x)=0有一個或零個實數根,因此將實數集分為2個區間,分別在這兩個區間上討論的正負,即可得出函數的單調性;
(2)當a=-1時,F(x)=f(x)•g(x)=e
x(-x+1),可以得出F(x)在(-∞,0)上為增函數,在(0,+∞)上為減函數,故函數的最大值為F(0)=1,可以求出符合題的實數t的取值范圍;
點評:(1)函數與方程的綜合運用在利用導數研究函數的單調性時更能體現它的作用.
(2)利用導數研究函數的單調性求函數的最值進而求出參數的范圍.

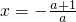
 ,+∞)單調減區間為(-∞,
,+∞)單調減區間為(-∞, )
) )單調減區間為(
)單調減區間為( ,+∞)
,+∞)

 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案 期末好成績系列答案
期末好成績系列答案