
已知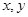 都是正數,
都是正數,
(1)若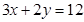 ,求
,求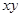 的最大值
的最大值
(2)若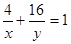 ,求
,求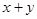 的最小值.
的最小值.
(1)6;(2)36.
【解析】
試題分析:(1)直接利用基本不等式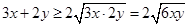 ,
,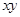 的最大值隨之而定;(2)如果直接利用基本不等式則有
的最大值隨之而定;(2)如果直接利用基本不等式則有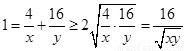 ①,
①,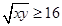 ,因此
,因此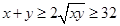 ②,這樣就可能得出
②,這樣就可能得出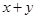 的最小值為32,實際上這個最小值是取不到的,因為不等式①取等號的條件是
的最小值為32,實際上這個最小值是取不到的,因為不等式①取等號的條件是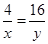 ,
,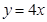 ,不等式②取等號的條件是
,不等式②取等號的條件是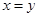 ,即不等式①②不能同時取等號,故
,即不等式①②不能同時取等號,故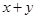 的最小值不是32.正確的解法是把
的最小值不是32.正確的解法是把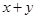 看作
看作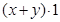 ,把其中的1用已知
,把其中的1用已知 代換,即
代換,即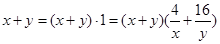 ,展開后就可以直接利用基本不等式求出結果.
,展開后就可以直接利用基本不等式求出結果.
試題解析:(1)xy=·3x·2y≤2=6 4分
當且僅當即時取“=”號.
所以當x=2,y=3時,xy取得最大值6 ..6分
(2)由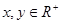 且
且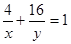 得
得
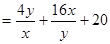
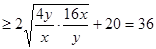 , ..10分
, ..10分
當且僅當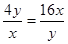 ,即x=12且y=24時,等號成立,
,即x=12且y=24時,等號成立,
所以x+y的最小值是36 12分
考點:基本不等式的應用.


 新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案 暑假銜接培優(yōu)教材浙江工商大學出版社系列答案
暑假銜接培優(yōu)教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源:2011-2012學年江蘇省蘇北四市(徐、連、淮、宿)高三元月調研測試數學試卷 題型:解答題
選修4-5:不等式選講(本小題滿分10分)已知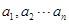 都是正數,且
都是正數,且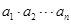 =1,求證:
=1,求證: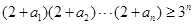
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省高三第二次月考理科數學試卷 題型:選擇題
給出下列命題,其中正確命題的個數是( )
①已知 都是正數,
都是正數, ,則
,則 ;②
;②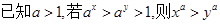 ;
;
③“ ,且
,且 ”是“
”是“ ”的充分不必要條件;
”的充分不必要條件;
④命題“ ,使得
,使得 ”的否定是“
”的否定是“ ,使得
,使得 ”.
”.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com