
 在矩形ABCD中,已知AD=2AB=2,點E是AD得中點,將△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.
在矩形ABCD中,已知AD=2AB=2,點E是AD得中點,將△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.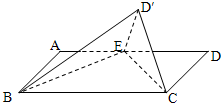 (1)證明:∵AD=2AB=2,E是AD的中點,
(1)證明:∵AD=2AB=2,E是AD的中點, ,
, ×1×1=
×1×1= ,∴V三棱錐B-D′EC=
,∴V三棱錐B-D′EC= ×
× ×
× =
= . …(9分)
. …(9分) ,
, ×
× ×1=
×1= ,∴V三棱錐E-D′BC=
,∴V三棱錐E-D′BC= ×
× ×h …(12分)
×h …(12分) .
. . …(14分)
. …(14分) ×
× ×
× =
= ,V三棱錐E-D′BC=
,V三棱錐E-D′BC= ×
× ×h,利用V三棱錐E-D′BC=V三棱錐B-D′EC,即可求得結論.
×h,利用V三棱錐E-D′BC=V三棱錐B-D′EC,即可求得結論.

 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
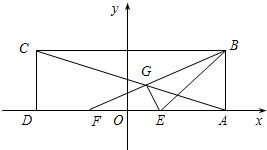 在矩形ABCD中,已知AD=6,AB=2,E、F為AD的兩個三等分點,AC和BF交于點G,△BEG的外接圓為⊙H.以DA所在直線為x軸,以DA中點O為坐標原點,建立如圖所示的平面直角坐標系.
在矩形ABCD中,已知AD=6,AB=2,E、F為AD的兩個三等分點,AC和BF交于點G,△BEG的外接圓為⊙H.以DA所在直線為x軸,以DA中點O為坐標原點,建立如圖所示的平面直角坐標系.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在矩形ABCD中,已知AB=3,AD=1,E、F分別是AB的兩個三等分點,AC,DF相交于點G,建立適當的平面直角坐標系:
如圖,在矩形ABCD中,已知AB=3,AD=1,E、F分別是AB的兩個三等分點,AC,DF相交于點G,建立適當的平面直角坐標系:查看答案和解析>>
科目:高中數學 來源: 題型:
 在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分別截取AE、AH、CG、CF都等于x,
在矩形ABCD中,已知AB=a,BC=b(a>b),在AB、AD、CD、CB上分別截取AE、AH、CG、CF都等于x,查看答案和解析>>
科目:高中數學 來源: 題型:
 在矩形ABCD中,已知AD=2AB=2,點E是AD得中點,將△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.
在矩形ABCD中,已知AD=2AB=2,點E是AD得中點,將△DEC沿CE折起到△D′EC的位置,使平面D′EC⊥平面BEC.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,在矩形ABCD中,已知AB=3AD,E,F為AB的兩個三等分點,AC,DF交于點G;
如圖,在矩形ABCD中,已知AB=3AD,E,F為AB的兩個三等分點,AC,DF交于點G;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com