
【題目】已知f(α)= ![]() .
.
(1)若α為第二象限角且f(α)=﹣ ![]() ,求
,求 ![]() 的值;
的值;
(2)若5f(α)=4f(3α+2β).試問tan(2α+β)tan(α+β)是否為定值(其中α≠kπ+ ![]() ,α+β≠kπ+
,α+β≠kπ+ ![]() ,2α+β≠kπ+
,2α+β≠kπ+ ![]() ,3α+2β≠kπ+
,3α+2β≠kπ+ ![]() ,k∈Z)?若是,請求出定值;否則,說明理由.
,k∈Z)?若是,請求出定值;否則,說明理由.
【答案】
(1)解:f(α)= ![]() =
= ![]()
![]() ,α為第二象限角,得
,α為第二象限角,得 ![]() .
.
![]() =
= ![]()
= 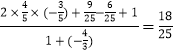
(2)解:∵5f(α)=4f(3α+2β),
∴5cos[(2α+β)﹣(α+β)]=4cos[(2α+β)+(α+β)].
可得:5[cos(2α+β)cos(α+β)+sin(2α+β)sin(α+β)]
=4[cos(2α+β)cos(α+β)﹣sin(2α+β)sin(α+β)],
化簡:cos(2α+β)cos(α+β)=﹣9sin(2α+β)sin(α+β).
又 ![]()
知cos(2α+β)cos(α+β)≠0
故tan(2α+β)tan(α+β)= ![]() .
.
綜上tan(2α+β)tan(α+β)是定值 ![]()
【解析】(1)直接化簡f(α)=cosα,由α為第二象限角求出sinα,再由二倍角公式化簡計算得答案;(2)由5f(α)=4f(3α+2β),得5cos[(2α+β)﹣(α+β)]=4cos[(2α+β)+(α+β)],進一步化簡可得cos(2α+β)cos(α+β)=﹣9sin(2α+β)sin(α+β),由已知條件可得cos(2α+β)cos(α+β)≠0,即可求出答案.


 全能測控一本好卷系列答案
全能測控一本好卷系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,當x≥0時,f(x)=x2﹣x
(1)求f(x)的解析式;
(2)畫出f(x)的圖象;
(3)若方程f(x)=k有4個解,求k的范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (x≠0).
(x≠0).
(1)證明函數f(x)為奇函數;
(2)判斷函數f(x)在[1,+∞)上的單調性,并說明理由;
(3)若x∈[﹣2,﹣3],求函數的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
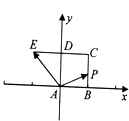
【題目】如圖,已知正方形ABCD的邊長為1,E在CD延長線上,且DE=CD.動點P從點A出發沿正方形ABCD的邊按逆進針方向運動一周回到A點,其中 ![]() =λ
=λ ![]() +μ
+μ ![]() ,則下列命題正確的是 . (填上所有正確命題的序號)
,則下列命題正確的是 . (填上所有正確命題的序號)
①當點P為AD中點時,λ+μ=1;
②λ+μ的最大值為3;
③若y為給定的正數,則一存在向量 ![]() 和實數x,使
和實數x,使 ![]() =x
=x ![]() +y
+y ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+α)(A>0,ω>0,﹣ ![]() <α<
<α< ![]() )的最小正周期是π,且當x=
)的最小正周期是π,且當x= ![]() 時,f(x)取得最大值2.
時,f(x)取得最大值2.
(1)求f(x)的解析式,并作出f(x)在[0,π]上的圖象(要列表);
(2)將函數f(x)的圖象向右平移m(m>0)個單位長度后得到函數y=g(x)的圖象,且y=g(x)是偶函數,求m的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某地一天中6時至14時的溫度變化曲線近似滿足函數y=Asin(ωx+φ)+B(其中 ![]() ),那么這一天6時至14時溫差的最大值是°C;與圖中曲線對應的函數解析式是 .
),那么這一天6時至14時溫差的最大值是°C;與圖中曲線對應的函數解析式是 . 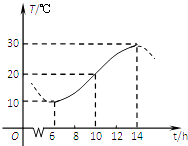
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個命題:
①三點確定一個平面;
②三條兩兩相交的直線確定一個平面;
③在空間上,與不共面四點A,B,C,D距離相等的平面恰有7個;
④兩個相交平面把空間分成四個區域.
其中真命題的序號是 (寫出所有真命題的序號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com