
【題目】已知橢圓 ![]() 上的動點P與其頂點
上的動點P與其頂點 ![]() ,
, ![]() 不重合. (Ⅰ)求證:直線PA與PB的斜率乘積為定值;
不重合. (Ⅰ)求證:直線PA與PB的斜率乘積為定值;
(Ⅱ)設點M,N在橢圓C上,O為坐標原點,當OM∥PA,ON∥PB時,求△OMN的面積.
【答案】解:(Ⅰ)證明:設P(x0 , y0),則 ![]() . 所以直線PA與PB的斜率乘積為
. 所以直線PA與PB的斜率乘積為 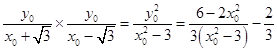 .…(4分)
.…(4分)
(Ⅱ)依題直線OM,ON的斜率乘積為- ![]() .
.
① 當直線MN的斜率不存在時,直線OM,ON的斜率為 ![]() ,設直線OM的方程
,設直線OM的方程
是 ![]() ,由
,由 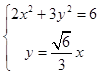 得
得 ![]() ,y=±1.
,y=±1.
取 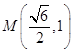 ,則
,則 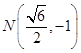 .所以△OMN的面積為
.所以△OMN的面積為 ![]() .
.
②當直線MN的斜率存在時,設直線MN的方程是y=kx+m,
由 ![]() 得(3k2+2)x2+6kmx+3m2﹣6=0.
得(3k2+2)x2+6kmx+3m2﹣6=0.
因為M,N在橢圓C上,
所以△=36k2m2﹣4(3k2+2)(3m2﹣6)>0,解得3k2﹣m2+2>0.
設M(x1 , y1),N(x2 , y2),則 ![]() ,
, ![]() .
. 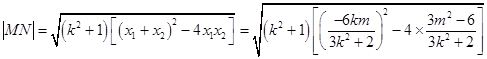 =
= 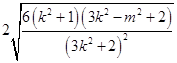 .
.
設點O到直線MN的距離為d,則 ![]() .
.
所以△OMN的面積為 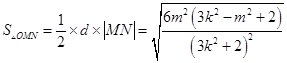 …①.
…①.
因為OM∥PA,ON∥PB,直線OM,ON的斜率乘積為- ![]() ,所以
,所以 ![]() .
.
所以 ![]() =
= ![]() .
.
由 ![]() ,得3k2+2=2m2…②
,得3k2+2=2m2…②
由①②,得 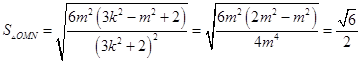 .
.
綜上所述, ![]()
【解析】(Ⅰ)設點設P(x0 , y0),從而可得直線PA與PB的斜率乘積為 ![]() (Ⅱ)設方程為y=kx+m,由兩點M,N滿足OM∥PA,ON∥PB及(Ⅰ)得直線OM,ON的斜率乘積為﹣
(Ⅱ)設方程為y=kx+m,由兩點M,N滿足OM∥PA,ON∥PB及(Ⅰ)得直線OM,ON的斜率乘積為﹣ ![]() ,可得到m、k的關系,再用弦長公式及距離公式,求出△OMN的底、高,表示:△OMN的面積即可.
,可得到m、k的關系,再用弦長公式及距離公式,求出△OMN的底、高,表示:△OMN的面積即可.


 一課一練課時達標系列答案
一課一練課時達標系列答案 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,an+1=1﹣ ![]() ,其中n∈N* .
,其中n∈N* .
(Ⅰ)設bn= ![]() ,求證:數列{bn}是等差數列,并求出{an}的通項公式an;
,求證:數列{bn}是等差數列,并求出{an}的通項公式an;
(Ⅱ)設Cn= ![]() ,數列{CnCn+2}的前n項和為Tn , 是否存在正整數m,使得Tn<
,數列{CnCn+2}的前n項和為Tn , 是否存在正整數m,使得Tn< ![]() 對于n∈N*恒成立,若存在,求出m的最小值,若不存在,請說明理由.
對于n∈N*恒成立,若存在,求出m的最小值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知M是直線l:x=﹣1上的動點,點F的坐標是(1,0),過M的直線l′與l垂直,并且l′與線段MF的垂直平分線相交于點N (Ⅰ)求點N的軌跡C的方程
(Ⅱ)設曲線C上的動點A關于x軸的對稱點為A′,點P的坐標為(2,0),直線AP與曲線C的另一個交點為B(B與A′不重合),直線P′H⊥A′B,垂足為H,是否存在一個定點Q,使得|QH|為定值?若存在,求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年微信用戶數量統計顯示,微信注冊用戶數量已經突破9.27億.微信用戶平均年齡只有26歲,97.7%的用戶在50歲以下,86.2%的用戶在18﹣36歲之間.為調查大學生這個微信用戶群體中每人擁有微信群的數量,現從北京市大學生中隨機抽取100位同學進行了抽樣調查,結果如下:
微信群數量 | 頻數 | 頻率 |
0至5個 | 0 | 0 |
6至10個 | 30 | 0.3 |
11至15個 | 30 | 0.3 |
16至20個 | a | c |
20個以上 | 5 | b |
合計 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)若從這100位同學中隨機抽取2人,求這2人中恰有1人微信群個數超過15個的概率;
(Ⅲ)以這100個人的樣本數據估計北京市的總體數據且以頻率估計概率,若從全市大學生中隨機抽取3人,記X表示抽到的是微信群個數超過15個的人數,求X的分布列和數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)滿足f(x)=f( ![]() )且當x∈[
)且當x∈[ ![]() ,1]時,f(x)=lnx,若當x∈[
,1]時,f(x)=lnx,若當x∈[ ![]() ]時,函數g(x)=f(x)﹣ax與x軸有交點,則實數a的取值范圍是( )
]時,函數g(x)=f(x)﹣ax與x軸有交點,則實數a的取值范圍是( )
A.[﹣ ![]() ,0]
,0]
B.[﹣πlnπ,0]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,﹣
,﹣ ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,P(x,y)為函數y=1+lnx圖象上一點,記直線OP的斜率k=f(x). (Ⅰ)若函數f(x)在區間(m,m+ ![]() )(m>0)上存在極值,求實數m的取值范圍;
)(m>0)上存在極值,求實數m的取值范圍;
(Ⅱ)當x≥1時,不等式f(x)≥ ![]() 恒成立,求實數t的取值范圍.
恒成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an},{bn}滿足bn=an+1﹣an(n=1,2,3,…).
(1)若bn=10﹣n,求a16﹣a5的值;
(2)若 ![]() 且a1=1,則數列{a2n+1}中第幾項最小?請說明理由;
且a1=1,則數列{a2n+1}中第幾項最小?請說明理由;
(3)若cn=an+2an+1(n=1,2,3,…),求證:“數列{an}為等差數列”的充分必要條件是“數列{cn}為等差數列且bn≤bn+1(n=1,2,3,…)”.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工藝品廠要設計一個如圖Ⅰ所示的工藝品,現有某種型號的長方形材料如圖Ⅱ所示,其周長為4m,這種材料沿其對角線折疊后就出現圖Ⅰ的情況.如圖,ABCD(AB>AD)為長方形的材料,沿AC折疊后AB'交DC于點P,設△ADP的面積為
S2 , 折疊后重合部分△ACP的面積為S1 .
(Ⅰ)設AB=xm,用x表示圖中DP的長度,并寫出x的取值范圍;
(Ⅱ)求面積S2最大時,應怎樣設計材料的長和寬?
(Ⅲ)求面積(S1+2S2)最大時,應怎樣設計材料的長和寬?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com