
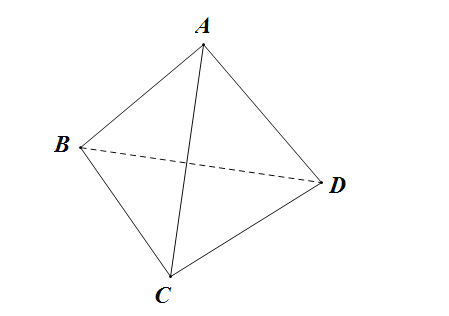
【題目】如圖,正四面體ABCD中,異面直線AB與CD所成的角為_______,直線AB與底面BCD所成角的余弦值為_______.
【答案】90° ![]()
【解析】
取CD中點E,連接AE、BE,作AF⊥BE于點F,
空1:根據等腰三角形的性質,結合線面垂直的判定定理和性質進行求解即可;
空2:根據線面垂直的性質和判定定理,結合線面角定義、銳角三角函數定義進行求解即可.
取CD中點E,連接AE、BE,作AF⊥BE于點F.
空1:因為![]() ,所以CD⊥AE,CD⊥BE,
,所以CD⊥AE,CD⊥BE,
AE![]() BE=E,
BE=E,![]() 平面ABE,∴CD⊥平面ABE,
平面ABE,∴CD⊥平面ABE,![]() 平面ABE,
平面ABE,
∴CD⊥AB,∴異面直線AB與CD所成的角為90°;
空2:∵CD⊥平面ABE,![]() 平面ABE,∴CD⊥AF,又AF⊥BE,
平面ABE,∴CD⊥AF,又AF⊥BE,
![]() 平面BCD,∴AF⊥平面BCD,
平面BCD,∴AF⊥平面BCD,
∴∠ABF是直線AB與底面BCD所成角,
正四面體ABCD中,因為AF⊥平面BCD,所以點F是三角形BCD的中心,
設正四面體的棱長為a,所以![]()
則 .
.

故答案為:90°;![]()


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知圓![]() 與
與![]() 軸相切于點(0,3),圓心在經過點(2,1)與點(﹣2,﹣3)的直線
軸相切于點(0,3),圓心在經過點(2,1)與點(﹣2,﹣3)的直線![]() 上.
上.
(1)求圓![]() 的方程;
的方程;
(2)圓![]() 與圓
與圓![]() :
:![]() 相交于M、N兩點,求兩圓的公共弦MN的長.
相交于M、N兩點,求兩圓的公共弦MN的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為發揮體育在核心素養時代的獨特育人價值,越來越多的中學已將某些體育項目納入到學生的必修課程,甚至關系到是否能拿到畢業證.某中學計劃在高一年級開設游泳課程,為了解學生對游泳的興趣,某數學研究性學習小組隨機從該校高一年級學生中抽取了100人進行調查,其中男生60人,且抽取的男生中對游泳有興趣的占![]() ,而抽取的女生中有15人表示對游泳沒有興趣.
,而抽取的女生中有15人表示對游泳沒有興趣.
(1)試完成下面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() 的把握認為“對游泳是否有興趣與性別有關”?
的把握認為“對游泳是否有興趣與性別有關”?
有興趣 | 沒興趣 | 合計 | |
男生 | |||
女生 | |||
合計 |
(2)已知在被抽取的女生中有6名高一(1)班的學生,其中3名對游泳有興趣,現在從這6名學生中隨機抽取3人,求至少有2人對游泳有興趣的概率.
(3)該研究性學習小組在調查中發現,對游泳有興趣的學生中有部分曾在市級和市級以上游泳比賽中獲獎,如下表所示.若從高一(8)班和高一(9)班獲獎學生中各隨機選取2人進行跟蹤調查,記選中的4人中市級以上游泳比賽獲獎的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列及數學期望.
的分布列及數學期望.
班級 |
|
|
|
|
|
|
|
|
|
|
|
市級比賽 獲獎人數 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
|
市級以上比賽獲獎人數 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
|
| 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)已知函數![]() ,函數
,函數![]() 的導函數為
的導函數為![]() .
.
①求函數![]() 的定義域;
的定義域;
②求函數![]() 的零點個數.
的零點個數.
(2)給出如下定義:如果![]() 是曲線
是曲線![]() 和曲線
和曲線![]() 的公共點,并且曲線
的公共點,并且曲線![]() 在點
在點![]() 處的切線與曲線
處的切線與曲線![]() 在點
在點![]() 處的切線重合,則稱曲線
處的切線重合,則稱曲線![]() 與曲線
與曲線![]() 在點
在點![]() 處相切,點
處相切,點![]() 叫曲線
叫曲線![]() 和曲線
和曲線![]() 的一個切點.試判斷曲線
的一個切點.試判斷曲線![]() :
:![]() 與曲線
與曲線![]() :
:![]() 是否在某點處相切?若是,求出所有切點的坐標;若不是,請說明理由.
是否在某點處相切?若是,求出所有切點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
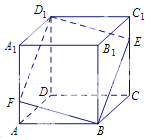
【題目】如圖所示,在正方體![]() 中,點
中,點![]() 是棱
是棱![]() 上的一個動點,平面
上的一個動點,平面![]() 交棱
交棱![]() 于點
于點![]() .給出下列命題:
.給出下列命題:
①存在點![]() ,使得
,使得![]() //平面
//平面![]() ;
;
②對于任意的點![]() ,平面
,平面![]() 平面
平面![]() ;
;
③存在點![]() ,使得
,使得![]() 平面
平面![]() ;
;
④對于任意的點![]() ,四棱錐
,四棱錐![]() 的體積均不變.
的體積均不變.
其中正確命題的序號是______.(寫出所有正確命題的序號).
查看答案和解析>>
科目:高中數學 來源: 題型:
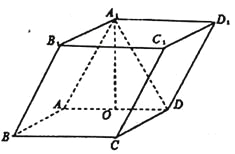
【題目】如圖,四棱柱![]() 中,底面
中,底面![]() 是矩形,且
是矩形,且![]() ,
, ![]() ,
, ![]() ,若
,若![]() 為
為![]() 的中點,且
的中點,且![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)線段![]() 上是否存在一點
上是否存在一點![]() ,使得二面角
,使得二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長;若不存在,說明理由.
的長;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 上一點
上一點![]() 到左右兩個焦點
到左右兩個焦點![]() 、
、![]() 的距離之和是4.
的距離之和是4.
(1)求橢圓的方程;
(2)已知過![]() 的直線與橢圓
的直線與橢圓![]() 交于
交于![]() 、
、![]() 兩點,且兩點與左右頂點不重合,若
兩點,且兩點與左右頂點不重合,若![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過
,過![]() 且與
且與![]() 軸垂直的直線被橢圓
軸垂直的直線被橢圓![]() 和圓
和圓![]() 截得的弦長分別為2和
截得的弦長分別為2和![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)已知動直線![]() 與拋物線
與拋物線![]() :
:![]() 相切(切點異于原點),且
相切(切點異于原點),且![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,問:橢圓
兩點,問:橢圓![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() ,若存在求出滿足條件的所有
,若存在求出滿足條件的所有![]() 點的坐標,若不存在,請說明理由.
點的坐標,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com