【題目】如圖，在三棱錐
中，
，
，D，E分別為BC，PD的中點，F為AB上一點，且
.
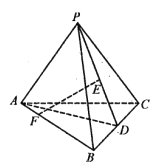
（1）求證：
平面PAD；
（2）求證：
平面PAC；
（3）若二面角
為60°，求三棱錐的體積.
【答案】（1）見解析（2）見解析（3）
【解析】
（1）根據一條直線與一個平面內的兩條相交直線都垂直，則該直線與此平面垂直，即證得；（2）根據平面外一條直線和此平面內的一條直線平行，那么這條直線和這個平面平行，在平面PAC中找一條直線與EF平行，即得證；（3）由二面角
為60°，可知
的面積，再由三棱錐的體積公式即得。
解：（1）證明：因為
，
，D是BC的中點，
所以
，
，
所以，
平面PAD.
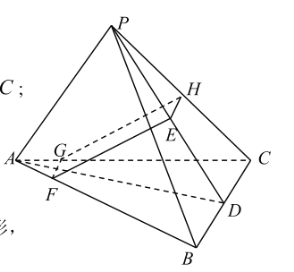
（2）證明：在AC上取一點G，使得
，
取PC的中點H連接FG、GH、HE，
在
中，有
，，則
；
在
中，E、H分別是PD、PC的中點，
則
，
；
所以，
，所以，四邊形EFGH為平行四邊形，
所以，
，又
平面PAC，
平面PAC，
所以，
平面PAC.
（3）由（1）知
，
，
所以
為二面角的平面角，即
，
在
中，
，
，所以
，
在
中，
，，所以
，
所以，
，
所以，三棱錐
的體積
.
科目：高中數學 來源： 題型：
【題目】在坐標平面上，縱橫坐標都是整數的點稱為整點.試證：存在一個同心圓的集合，使得：（1）每個整點都在此集體的某一圓周上；（2）此集合的每個圓周上.有且只有一個整點.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】經過市場調查，某種商品在銷售中有如下關系：第x（
）天的銷售價格（單位：元/件）為
，第x天的銷售量（單位：件）為
（
為常數），且在第20天該商品的銷售收入為600元（銷售收入=銷售價格×銷售量）.
（1）求a的值，并求第15天該商品的銷售收入；
（2）求在這30天中，該商品日銷售收入y的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
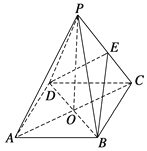
【題目】如圖所示，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，底面邊長為a，E是PC的中點．
(1)求證：平面PAC⊥平面BDE；
(2)若二面角E－BD－C為30°，求四棱錐P－ABCD的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】暑假期間，某旅行社為吸引游客去某風景區旅游，推出如下收費標準：若旅行團人數不超過30，則每位游客需交費用600元；若旅行團人數超過30，則游客每多1人，每人交費額減少10元，直到達到70人為止.
（1）寫出旅行團每人需交費用
（單位：元）與旅行團人數
之間的函數關系式；
（2）旅行團人數為多少時，旅行社可以從該旅行團獲得最大收入？最大收入是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知實數x，y滿足x3＜y3，則下列不等式中恒成立的是（ ）
A. （
）x＞（）y B. ln（x2+1）＞ln（y2+1）
C. 
D. tanx＞tany
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知一家公司生產某種品牌服裝的年固定成本為10萬元，每生產1千件需另投入2.7萬元．設該公司一年內共生產該品牌服裝x千件并全部銷售完，每千件的銷售收入為
萬元，且
.
（1）寫出年利潤W（萬元）關于年產量x（千件）的函數解析式；
（2）年產量為多少千件時，該公司在這一品牌服裝的生產中所獲得利潤最大？（注：年利潤=年銷售收入﹣年總成本）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現對一塊邊長8米的正方形場地ABCD進行改造，點E為線段BC的中點，點F在線段CD或AD上（異于A，C），設
（米），
的面積記為
（平方米），其余部分面積記為
（平方米）.
（1）當
（米）時，求
的值；
（2）求函數的最大值；
（3）該場地中部分改造費用為
（萬元），其余部分改造費用為
（萬元），記總的改造費用為W（萬元），求W取最小值時x的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位共有老、中、青職工430人,其中青年職工160人，中年職工人數是老年職工人數的2倍。為了解職工身體狀況，現采用分層抽樣方法進行調查，在抽取的樣本中有青年職工32人，則該樣本中的老年職工人數為
A. 9 B. 18 C. 27 D. 36
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com