
【題目】函數![]() 的值域為_________________.
的值域為_________________.
【答案】[-1,1)
【解析】
由題可得![]() ,由
,由![]() 易得0<
易得0<![]() ≤2,
≤2,
故y∈[-1,1),所以函數![]() 的值域為[-1,1) .
的值域為[-1,1) .
【解題必備】(1)在高考中考查函數的定義域時多以客觀題形式呈現,難度不大.求函數定義域的三種常考類型及求解策略:①已知函數的解析式:構建使解析式有意義的不等式(組)求解;②對于抽象函數:若已知函數f(x)的定義域為[a,b],則復合函數f(g(x))的定義域由a≤g(x)≤b求出,若已知函數f(g(x))的定義域為[a,b],則f(x)的定義域為g(x)在x∈[a,b]時的值域;③對于實際問題:既要使構建的函數解析式有意義,又要考慮實際問題的要求.
(2)求函數定義域的注意點:①不要對解析式進行化簡變形,以免定義域變化;②當一個函數由有限個基本初等函數的和、差、積、商的形式構成時,定義域一般是各個基本初等函數定義域的交集;③定義域是一個集合,要用集合或區間表示,若用區間表示,不能用“或”連接,而應該用并集符號“∪”連接.
(3)求函數值域的基本方法:①觀察法,通過對函數解析式的簡單變形,利用熟知的基本函數的值域,或利用函數圖象的“最高點”和“最低點”,觀察求得函數的值域;②利用常見函數的值域,一次函數的值域為![]() ,反比例函數的值域為
,反比例函數的值域為![]() ,指數函數的值域為
,指數函數的值域為![]() ,對數函數的值域為
,對數函數的值域為![]() ,正、余弦函數的值域為
,正、余弦函數的值域為![]() ,正切函數的值域為
,正切函數的值域為![]() ;③分離常數法,將形如
;③分離常數法,將形如![]() (a≠0)的函數分離常數,結合x的取值范圍確定函數的值域;④換元法,對某些無理函數或其他函數,通過適當的換元,把它們化為我們熟悉的函數,再用有關方法求值域;⑤配方法,對二次函數型的解析式可以先進行配方,在充分注意到自變量取值范圍的情況下,利用求二次函數的值域的方法求函數的值域;⑥數形結合法,作出函數圖象,找出自變量對應的范圍或分析條件的幾何意義,在圖上找出值域;⑦單調性法(也可結合導數),函數單調性的變化是求最值和值域的依據,根據函數的單調區間判斷其單調性,進而求函數的最值和值域;⑧基本不等式法,利用基本不等式
(a≠0)的函數分離常數,結合x的取值范圍確定函數的值域;④換元法,對某些無理函數或其他函數,通過適當的換元,把它們化為我們熟悉的函數,再用有關方法求值域;⑤配方法,對二次函數型的解析式可以先進行配方,在充分注意到自變量取值范圍的情況下,利用求二次函數的值域的方法求函數的值域;⑥數形結合法,作出函數圖象,找出自變量對應的范圍或分析條件的幾何意義,在圖上找出值域;⑦單調性法(也可結合導數),函數單調性的變化是求最值和值域的依據,根據函數的單調區間判斷其單調性,進而求函數的最值和值域;⑧基本不等式法,利用基本不等式![]() (a>0,b>0)求最值,注意應用基本不等式的條件是“一正二定三相等”;⑨判別式法,將函數轉化為二次方程,利用Δ≥0,由此確定函數的值域,利用判別式求函數值的范圍,常用于一些“分式”函數、“無理”函數等,使用此法要特別注意自變量的取值范圍;⑩有界性法,充分利用三角函數或一些代數表達式的有界性,求出值域.
(a>0,b>0)求最值,注意應用基本不等式的條件是“一正二定三相等”;⑨判別式法,將函數轉化為二次方程,利用Δ≥0,由此確定函數的值域,利用判別式求函數值的范圍,常用于一些“分式”函數、“無理”函數等,使用此法要特別注意自變量的取值范圍;⑩有界性法,充分利用三角函數或一些代數表達式的有界性,求出值域.


科目:高中數學 來源: 題型:
【題目】2017年“十一”期間,高速公路車輛較多.某調查公司在一服務區從七座以下小型汽車中按進服務區的先后每間隔50輛就抽取一輛的抽樣方法抽取40名駕駛員進行詢問調查,將他們在某段高速公路的車速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如圖的頻率分布直方圖.
,后得到如圖的頻率分布直方圖.

(1)求這40輛小型車輛車速的眾數和中位數的估計值;
(2)若從車速在![]() 的車輛中任抽取2輛,求車速在
的車輛中任抽取2輛,求車速在![]() 的車輛恰有一輛的概率.
的車輛恰有一輛的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數![]() 定義域為
定義域為![]() ,且對任意實數
,且對任意實數![]() ,有
,有![]() ,則稱
,則稱![]() 為“
為“![]() 形函數”,若函數
形函數”,若函數![]() 定義域為
定義域為![]() ,函數
,函數![]() 對任意
對任意![]() 恒成立,且對任意實數
恒成立,且對任意實數![]() ,有
,有![]() ,則稱為“對數
,則稱為“對數![]() 形函數” .
形函數” .
(1)試判斷函數![]() 是否為“
是否為“![]() 形函數”,并說明理由;
形函數”,并說明理由;
(2)若![]() 是“對數
是“對數![]() 形函數”,求實數
形函數”,求實數![]() 的取值范圍;
的取值范圍;
(3)若![]() 是“
是“![]() 形函數”,且滿足對任意
形函數”,且滿足對任意![]() ,有
,有![]() ,問
,問![]() 是否為“對數
是否為“對數![]() 形函數”?證明你的結論.
形函數”?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區高考實行新方案,規定:語文、數學和英語是考生的必考科目,考生還須從物理、化學、生物、歷史、地理和政治六個科目中選取三個科目作為選考科目,若一名學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定.例如,學生甲選擇“物理、化學和生物”三個選考科目,則學生甲的選考方案確定,“物理、化學和生物”為其選考方案.
某學校為了了解高一年級420名學生選考科目的意向,隨機選取30名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
選考方案待確定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 選考方案確定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
選考方案待確定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(Ⅱ)假設男生、女生選擇選考科目是相互獨立的.從選考方案確定的8位男生隨機選出1人,從選考方案確定的10位女生中隨機選出1人,試求該男生和該女生的選考方案中都含有歷史科目的概率;
(Ⅲ)從選考方案確定的8名男生隨機選出2名,設隨機變量兩名男生選考方案相同時![]() ,兩名男生選考方案不同時
,兩名男生選考方案不同時![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() )依次為函數
)依次為函數![]() 圖像上的點,點列
圖像上的點,點列![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() )依次為
)依次為![]() 軸正半軸上的點,其中
軸正半軸上的點,其中![]() (
(![]() ),對于任意
),對于任意![]() ,點
,點![]() 、
、![]() 、
、![]() 構成一個頂角的頂點為
構成一個頂角的頂點為![]() 的等腰三角形.
的等腰三角形.
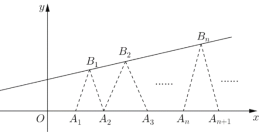
(1)證明:數列![]() 是等差數列;
是等差數列;
(2)證明:![]() 為常數,并求出數列
為常數,并求出數列![]() 的前
的前![]() 項和
項和![]() ;
;
(3)在上述等腰三角形![]() 中,是否存在直角三角形?若存在,求出
中,是否存在直角三角形?若存在,求出![]() 值,若不存在,請說明理由.
值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銷售甲、乙兩種商品所得利潤分別是![]() 萬元,它們與投入資金
萬元,它們與投入資金![]() 萬元的關系分別為
萬元的關系分別為![]() ,
,![]() ,(其中
,(其中![]() 都為常數),函數
都為常數),函數![]() 對應的曲線
對應的曲線![]() 、
、![]() 如圖所示.
如圖所示.

(1)求函數![]() 與
與![]() 的解析式;
的解析式;
(2)若該商場一共投資4萬元經銷甲、乙兩種商品,求該商場所獲利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】春節過后,某市教育局從全市高中生中抽去了100人,調查了他們的壓歲錢收入情況,按照金額(單位:百元)分成了以下幾組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .統計結果如下表所示:
.統計結果如下表所示:
![]()
該市高中生壓歲錢收入![]() 可以認為服從正態分布
可以認為服從正態分布![]() ,用樣本平均數
,用樣本平均數![]() (每組數據取區間的中點值)作為
(每組數據取區間的中點值)作為![]() 的估計值.
的估計值.
(1)求樣本平均數![]() ;
;
(2)求![]() ;
;
(3)某文化公司贊助了市教育局的這次社會調查活動,并針對該市的高中生制定了贈送“讀書卡”的活動,贈送方式為:壓歲錢低于![]() 的獲贈兩次讀書卡,壓歲錢不低于
的獲贈兩次讀書卡,壓歲錢不低于![]() 的獲贈一次讀書卡.已知每次贈送的讀書卡張數及對應的概率如下表所示:
的獲贈一次讀書卡.已知每次贈送的讀書卡張數及對應的概率如下表所示:

現從該市高中生中隨機抽取一人,記![]() (單位:張)為該名高中生獲贈的讀書卡的張數,求
(單位:張)為該名高中生獲贈的讀書卡的張數,求![]() 的分布列及數學期望.
的分布列及數學期望.
參考數據:若![]() ,則
,則![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C對應的邊分別是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面積S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com