
已知函數
(Ⅰ)若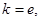 試確定函數
試確定函數 的單調區間;
的單調區間;
(Ⅱ)若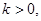 且對于任意
且對于任意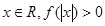 恒成立,試確定實數
恒成立,試確定實數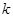 的取值范圍;
的取值范圍;
(Ⅲ)設函數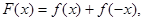 求證:
求證: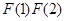
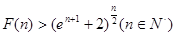 .
.
(Ⅰ)單調遞增區間是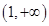 ,單調遞減區間是
,單調遞減區間是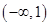 ;(Ⅱ)
;(Ⅱ)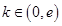 ;(Ⅲ)見解析.
;(Ⅲ)見解析.
解析試題分析:(Ⅰ)求出函數的導數,令導數大于零解得單調增區間,令導數小于零得單調減區間;(Ⅱ)先可得知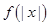 是偶函數,于是
是偶函數,于是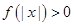 對任意
對任意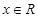 成立等價于
成立等價于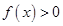 對任意
對任意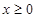 成立,令導數等于零得
成立,令導數等于零得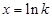 ,然后對
,然后對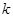 在
在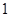 處斷開進行討論;(Ⅲ)先求得
處斷開進行討論;(Ⅲ)先求得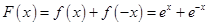 ,并證明
,并證明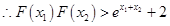 ,然后列舉累乘即可證明.
,然后列舉累乘即可證明.
試題解析:(Ⅰ)由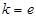 得
得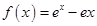 ,所以
,所以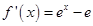 .
.
由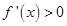 得
得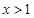 ,故
,故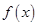 的單調遞增區間是
的單調遞增區間是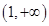 , 3分
, 3分
由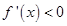 得
得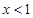 ,故
,故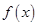 的單調遞減區間是
的單調遞減區間是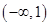 . 4分
. 4分
(Ⅱ)由 可知
可知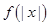 是偶函數.
是偶函數.
于是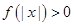 對任意
對任意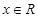 成立等價于
成立等價于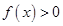 對任意
對任意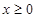 成立. 5分
成立. 5分
由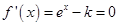 得
得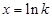 .
.
①當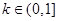 時,
時,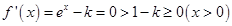 .此時
.此時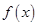 在
在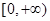 上單調遞增.故
上單調遞增.故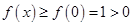 ,符合題意. 6分
,符合題意. 6分
②當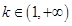 時,
時,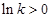 .當
.當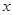 變化時
變化時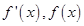 的變化情況如下表:
的變化情況如下表: