
 ,點P隨線段MN的運(yùn)動而變化.
,點P隨線段MN的運(yùn)動而變化. ,是否存在這樣的直線l,使四邊形OASB的對角線相等(即|OS|=|AB|)?若存在,求出直線l的方程;若不存在,試說明理由.
,是否存在這樣的直線l,使四邊形OASB的對角線相等(即|OS|=|AB|)?若存在,求出直線l的方程;若不存在,試說明理由.
 解:(1)設(shè)M(x,0),N(0,y),P(x,y) 因為|MN|=5,所以x2+y2=25(*)
解:(1)設(shè)M(x,0),N(0,y),P(x,y) 因為|MN|=5,所以x2+y2=25(*)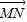 所成的比為
所成的比為
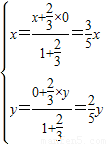 ∴
∴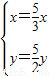
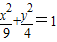 即為所求的方程
即為所求的方程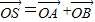 ,所以四邊形OASB為平行四邊形,若存在l使得|
,所以四邊形OASB為平行四邊形,若存在l使得| |=|
|=|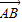 |,則四邊形OASB為矩形
|,則四邊形OASB為矩形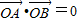 若l的斜率不存在,直線l的方程為x=2,由
若l的斜率不存在,直線l的方程為x=2,由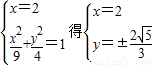
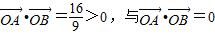 矛盾,故l的斜率存在.
矛盾,故l的斜率存在.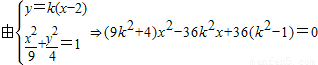
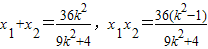 ①
①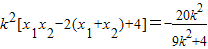 ②
②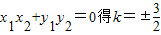



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
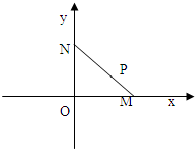 如圖,線段MN的兩個端點M、N分別在x軸、y 軸上滑動,|MN|=5,點P是線段MN上一點,且
如圖,線段MN的兩個端點M、N分別在x軸、y 軸上滑動,|MN|=5,點P是線段MN上一點,且| MP |
| 2 |
| 3 |
| PN |
| OS |
| OA |
| OB |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年福建省長泰一中高二下學(xué)期期中考試?yán)砜茢?shù)學(xué) 題型:解答題
(本小題滿分14分)
如圖,線段MN的兩個端點M.N分別在x軸.y 軸上滑動, ,點P是線段MN上一點,且
,點P是線段MN上一點,且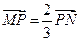 ,點P隨線段MN的運(yùn)動而變化.
,點P隨線段MN的運(yùn)動而變化.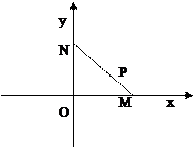
(1)求點P的軌跡C的方程;
(2)過點(2,0)作直線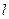 ,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)
,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)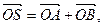 是否存在這樣的直線
是否存在這樣的直線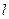 ,使四邊形
,使四邊形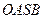 的對角線相等(即
的對角線相等(即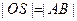 )?若存在,求出直線
)?若存在,求出直線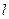 的方程;若不存在,試說明理由.
的方程;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年福建省高二下學(xué)期期中考試?yán)砜茢?shù)學(xué) 題型:解答題
(本小題滿分14分)
如圖,線段MN的兩個端點M.N分別在x軸.y 軸上滑動,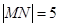 ,點P是線段MN上一點,且
,點P是線段MN上一點,且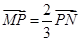 ,點P隨線段MN的運(yùn)動而變化.
,點P隨線段MN的運(yùn)動而變化.
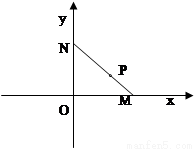
(1)求點P的軌跡C的方程;
(2)過點(2,0)作直線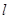 ,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)
,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)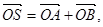 是否存在這樣的直線
是否存在這樣的直線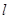 ,使四邊形
,使四邊形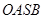 的對角線相等(即
的對角線相等(即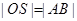 )?若存在,求出直線
)?若存在,求出直線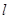 的方程;若不存在,試說明理由.
的方程;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
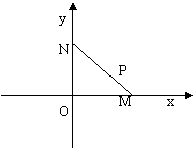
(本小題滿分14分)如圖,線段MN的兩個端點M.N分別在x軸.y 軸上滑動,![]() ,點P是線段MN上一點,且
,點P是線段MN上一點,且![]() ,點P隨線段MN的運(yùn)動而變化.
,點P隨線段MN的運(yùn)動而變化.
(1)求點P的軌跡C的方程;
 (2)過點(2,0)作直線
(2)過點(2,0)作直線![]() ,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)
,與曲線C交于A.B兩點,O是坐標(biāo)原點,設(shè)![]() 是否存在這樣的直線
是否存在這樣的直線![]() ,使四邊形
,使四邊形![]() 的對角線相等(即
的對角線相等(即![]() )?若存在,求出直線
)?若存在,求出直線![]() 的方程;若不存在,試說明理由.
的方程;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2008-2009學(xué)年浙江省溫州市三溪中學(xué)高二期中數(shù)學(xué)試卷(理科)(選修2-1)(解析版) 題型:解答題
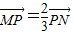 ,點P隨線段MN的運(yùn)動而變化.
,點P隨線段MN的運(yùn)動而變化.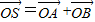 ,是否存在這樣的直線l,使四邊形OASB的對角線相等(即|OS|=|AB|)?若存在,求出直線l的方程;若不存在,試說明理由.
,是否存在這樣的直線l,使四邊形OASB的對角線相等(即|OS|=|AB|)?若存在,求出直線l的方程;若不存在,試說明理由.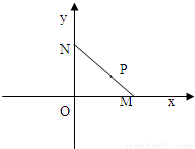
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com