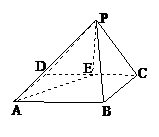
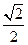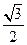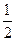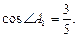如圖,底面是正方形的四棱錐
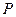
–
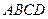
,平面
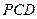
⊥平面
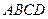
,
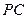
=
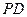
=
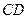
=2.
(I)求證:
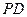
⊥
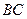
;
(II)求直線
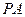
與平面
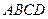
所成的角的正弦值.
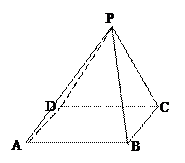
(II)
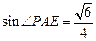
(I)證明:∵平面
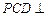
平面
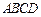
,
平面
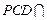
平面
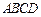
=
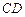
,
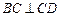
,∴
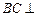
平面
,
又
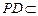
平面
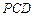
,∴
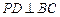
..………………………………7 分
(II)取
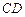
中點
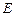
,由
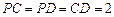
得
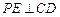
,
又平面
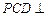
平面
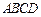
,故
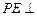
平面
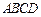
,
∴
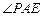
就是直線
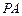
與平面
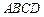
所成的角.
∵
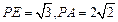
,∴
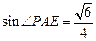
. ……………………………………14 分
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,直角梯形ABCE中,
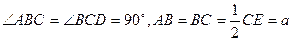
,D是CE的中點,點M和點N在
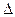
ADE繞AD向上翻折的過程中,分別以
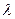
的速度,同時從點A和點B沿AE和BD各自勻速行進,t 為行進時間,0
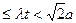
。
(1) 求直線AE與平面CDE所成的角;
(2) 求證:MN//平面CDE。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,正三棱柱
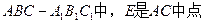
.
(1)求證:平面
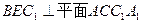
;
(2)求證:
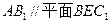
;
(3)若
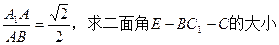
.
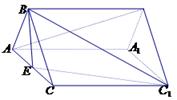
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
在直三棱柱
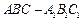
中,
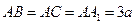
,
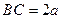
,
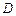
是
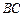
的中點,
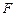
是
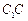
上一點,且
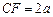
.
(1)求證:
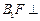
平面
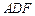
;
(2)求三棱錐
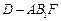
的體積;
(3)試在
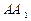
上找一點
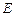
,使得
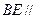
平面
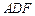
.
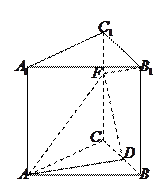
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,四棱錐
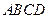
中,底面
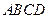
是正方形,
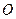
是正方形
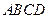
的中心,
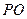
底面
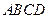
,
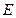
是
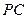
的中點.
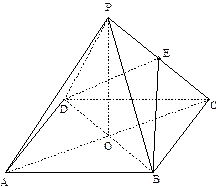
求證:(Ⅰ)
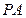
∥平面
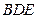
;
(Ⅱ)平面
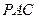
平面
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,在三棱錐P-ABC中,AB⊥BC,AB=BC=PA=a,點O、D分別是AC、PC的中點,OP⊥底面ABC。
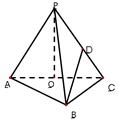
(1)求三棱錐P-ABC的體積;
(2)求異面直線PA與BD所成角余弦值的大小。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
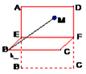
正方形
ABCD邊長為2,
E、
F分別是
AB和
CD的中點,將正方形沿
EF折成直二面角(如圖),
M為矩形
AEFD內(nèi)一點,如果∠
MBE=∠
MBC,
MB和平面
BCF所成角的正切值為
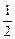
,那么點
M到直線
EF的距離為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
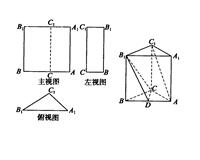
已知三棱柱
ABC—
A1B1C1的三視圖如圖所示,其中主視圖
AA1B1B和左視圖
B1BCC1均為矩形,俯高圖△
A1B1C1中,
A1C1=3,
A1B1=5,
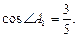
(1)在三棱柱
ABC—
A1B1C1中,求證:
BC⊥
AC1;
(2)在三棱柱
ABC—
A1B1C1中,若
D是底邊
AB的中點,求證:
AC1∥平面
CDB1;
(3)若三棱柱的高為5,求三視圖中左視圖的面積.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
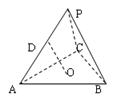
如下圖,在正三棱錐P-ABC中,D是側(cè)棱PA的中點,O是底面ABC的中心,則下列四個結(jié)論中正確的是( )
| A.OA∥平面PBC | B.OD⊥PA | C.OD⊥AC | D.PA=2OD |
查看答案和解析>>

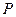 –
–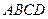 ,平面
,平面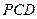 ⊥平面
⊥平面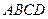 ,
,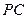 =
=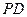 =
=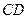 =2.
=2.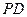 ⊥
⊥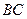 ;
;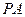 與平面
與平面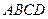 所成的角的正弦值.
所成的角的正弦值.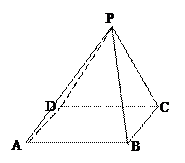
 科學(xué)實驗活動冊系列答案
科學(xué)實驗活動冊系列答案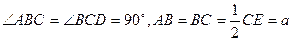 ,D是CE的中點,點M和點N在
,D是CE的中點,點M和點N在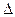 ADE繞AD向上翻折的過程中,分別以
ADE繞AD向上翻折的過程中,分別以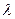 的速度,同時從點A和點B沿AE和BD各自勻速行進,t 為行進時間,0
的速度,同時從點A和點B沿AE和BD各自勻速行進,t 為行進時間,0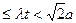 。
。
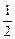 ,那么點M到直線EF的距離為( )
,那么點M到直線EF的距離為( )