
【題目】已知函數![]() .
.
(1)若![]() ,求證:
,求證:![]() .
.
(2)討論函數![]() 的極值;
的極值;
(3)是否存在實數![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立?若存在,求出
上恒成立?若存在,求出![]() 的最小值;若不存在,請說明理由.
的最小值;若不存在,請說明理由.
【答案】(1)證明見解析;(2)見解析;(3)存在,1.
【解析】
(1)![]() ,求出
,求出![]() 單調區間,進而求出
單調區間,進而求出![]() ,即可證明結論;
,即可證明結論;
(2)對![]() (或
(或![]() )是否恒成立分類討論,若恒成立,沒有極值點,若不恒成立,求出
)是否恒成立分類討論,若恒成立,沒有極值點,若不恒成立,求出![]() 的解,即可求出結論;
的解,即可求出結論;
(3)令![]() ,可證
,可證![]() 恒成立,而
恒成立,而![]() ,由(2)得,
,由(2)得,![]() 在
在![]() 為減函數,
為減函數,![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 都存在
都存在![]() ,不滿足
,不滿足![]() ,當
,當![]() 時,設
時,設![]() ,且
,且![]() ,只需求出
,只需求出![]() 在
在![]() 單調遞增時
單調遞增時![]() 的取值范圍即可.
的取值范圍即可.
(1)![]() ,
,![]() ,
,
![]() ,當
,當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,∴
,∴![]() ,故
,故![]() .
.
(2)由題知,![]() ,
,![]() ,
,
①當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,沒有極值;
上單調遞減,沒有極值;
②當![]() 時,
時,![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
故![]() 在
在![]() 處取得極小值
處取得極小值![]() ,無極大值.
,無極大值.
(3)不妨令![]() ,
,
設![]() 在
在![]() 恒成立,
恒成立,
![]() 在
在![]() 單調遞增,
單調遞增,![]() ,
,
![]() 在
在![]() 恒成立,
恒成立,
所以,當![]() 時,
時,![]() ,
,
由(2)知,當![]() 時,
時,![]() 在
在![]() 上單調遞減,
上單調遞減,
![]() 恒成立;
恒成立;
所以不等式![]() 在
在![]() 上恒成立,只能
上恒成立,只能![]() .
.
當![]() 時,
時,![]() ,由(1)知
,由(1)知![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,不滿足題意.
,不滿足題意.
當![]() 時,設
時,設![]() ,
,
因為![]() ,所以
,所以![]() ,
,
![]() ,
,
即![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,所以
,所以![]() 時,
時,![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
故存在![]() ,使得不等式
,使得不等式![]() 在
在![]() 上恒成立,
上恒成立,
此時![]() 的最小值是1.
的最小值是1.


 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:高中數學 來源: 題型:
【題目】設函數![]() ,(
,(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,求實數a、m的值;
,求實數a、m的值;
(2)若![]() 對任意
對任意![]() 恒成立,求實數a的取值范圍;
恒成立,求實數a的取值范圍;
(3)關于x的方程![]() 能否有三個不同的實根?證明你的結論.
能否有三個不同的實根?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以直角坐標系的原點
為參數).以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立坐標系,曲線
軸的正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,與
兩點,與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙三人在政治、歷史、地理、物理、化學、生物、技術7門學科中任選3門.若同學甲必選物理,則下列說法正確的是( )
A.甲、乙、丙三人至少一人選化學與全選化學是對立事件
B.甲的不同的選法種數為15
C.已知乙同學選了物理,乙同學選技術的概率是![]()
D.乙、丙兩名同學都選物理的概率是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,如圖,
中,如圖,![]() 分別是正方形
分別是正方形![]() ,
,![]() 的中心.則下列結論正確的是( )
的中心.則下列結論正確的是( )
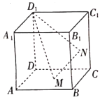
A.平面![]() 與
與![]() 的交點是
的交點是![]() 的中點
的中點
B.平面![]() 與
與![]() 的交點是
的交點是![]() 的三點分點
的三點分點
C.平面![]() 與
與![]() 的交點是
的交點是![]() 的三等分點
的三等分點
D.平面![]() 將正方體分成兩部分的體積比為1∶1
將正方體分成兩部分的體積比為1∶1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex-x2 -kx(其中e為自然對數的底,k為常數)有一個極大值點和一個極小值點.
(1)求實數k的取值范圍;
(2)證明:f(x)的極大值不小于1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應國家號召,促進垃圾分類,某校組織了高三年級學生參與了“垃圾分類,從我做起”的知識問卷作答隨機抽出男女各20名同學的問卷進行打分,作出如圖所示的莖葉圖,成績大于70分的為“合格”.
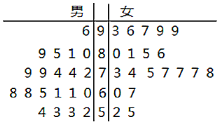
(Ⅰ)由以上數據繪制成2×2聯表,是否有95%以上的把握認為“性別”與“問卷結果”有關?
男 | 女 | 總計 | |
合格 | |||
不合格 | |||
總計 |
(Ⅱ)從上述樣本中,成績在60分以下(不含60分)的男女學生問卷中任意選2個,記來自男生的個數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
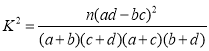
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,若橢圓經過點
,若橢圓經過點![]() ,且△PF1F2的面積為2.
,且△PF1F2的面積為2.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設斜率為1的直線![]() 與以原點為圓心,半徑為
與以原點為圓心,半徑為![]() 的圓交于A,B兩點,與橢圓C交于C,D兩點,且
的圓交于A,B兩點,與橢圓C交于C,D兩點,且![]() (
(![]() ),當
),當![]() 取得最小值時,求直線
取得最小值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com