
【題目】如圖所示,M,N,K分別是正方體ABCD—A1B1C1D1的棱AB,CD,C1D1的中點.

求證:(1)AN∥平面A1MK;
(2)平面A1B1C⊥平面A1MK.
【答案】(1)見解析(2)見解析
【解析】試題分析: ![]() 要證明
要證明![]() 平面
平面![]() ,只需要證明
,只需要證明![]() 平行于平面
平行于平面![]() 內的一條直線,容易證明
內的一條直線,容易證明![]() ,從而得到證明;
,從而得到證明;
![]() 要證明
要證明![]() 平面
平面![]() ,只需要證明平面
,只需要證明平面![]() 內的直線
內的直線![]() 垂直于平面
垂直于平面![]() 即可,而
即可,而![]() 容易證明,從而問題得到解決;
容易證明,從而問題得到解決;
解析:證明 (1)如圖所示,連接NK.
在正方體ABCD—A1B1C1D1中,
∵四邊形AA1D1D,DD1C1C都為正方形,
∴AA1∥DD1,AA1=DD1,C1D1∥CD,C1D1=CD.[2分]
∵N,K分別為CD,C1D1的中點,

∴DN∥D1K,DN=D1K,
∴四邊形DD1KN為平行四邊形.
∴KN∥DD1,KN=DD1,∴AA1∥KN,AA1=KN.
∴四邊形AA1KN為平行四邊形.∴AN∥A1K.
∵A1K平面A1MK,AN平面A1MK,
∴AN∥平面A1MK.
(2)如圖所示,連接BC1.

在正方體ABCD—A1B1C1D1中,AB∥C1D1,AB=C1D1.
∵M,K分別為AB,C1D1的中點,
∴BM∥C1K,BM=C1K.
∴四邊形BC1KM為平行四邊形.∴MK∥BC1.
在正方體ABCD—A1B1C1D1中,A1B1⊥平面BB1C1C,
BC1平面BB1C1C,∴A1B1⊥BC1.
∵MK∥BC1,∴A1B1⊥MK.
∵四邊形BB1C1C為正方形,∴BC1⊥B1C.
∴MK⊥B1C.
∵A1B1平面A1B1C,B1C平面A1B1C,A1B1∩B1C=B1,∴MK⊥平面A1B1C.
又∵MK平面A1MK,
∴平面A1B1C⊥平面A1MK.


科目:高中數學 來源: 題型:
【題目】某旅游城市為向游客介紹本地的氣溫情況,繪制了一年中各月平均最高氣溫和平均最低氣溫的雷達圖. 圖中A點表示十月的平均最高氣溫約為![]() ,B點表示四月的平均最低氣溫約為
,B點表示四月的平均最低氣溫約為![]() . 下面敘述不正確的是 ( )
. 下面敘述不正確的是 ( )

A. 各月的平均最低氣溫都在![]() 以上
以上
B. 七月的平均溫差比一月的平均溫差大
C. 三月和十一月的平均最高氣溫基本相同
D. 平均最高氣溫高于![]() 的月份有5個
的月份有5個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】判斷下列兩圓的位置關系.
(1)C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0;___________
(2)C1:x2+y2-2y=0,C2:x2+y2-2![]() x-6=0;___________
x-6=0;___________
(3)C1:x2+y2-4x-6y+9=0,C2:x2+y2+12x+6y-19=0;___________
(4)C1:x2+y2+2x-2y-2=0,C2:x2+y2-4x-6y-3=0.___________
(5)x2+y2=9和x2+y2-8x+6y+9=0 ________________
(6)圓C1:x2+y2-2x-6y-6=0與圓C2:x2+y2-4x+2y+4=0______
(7)圓x2+y2+6x-7=0和圓x2+y2+6y-27=0 ____________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列A: ![]() ,
, ![]() ,…
,… ![]() (N≥2)。如果對小于n(2≤n≤N)的每個正整數k都有
(N≥2)。如果對小于n(2≤n≤N)的每個正整數k都有 ![]() <
< ![]() ,則稱n是數列A的一個“G時刻”。記“G(A)是數列A 的所有“G時刻”組成的集合。
,則稱n是數列A的一個“G時刻”。記“G(A)是數列A 的所有“G時刻”組成的集合。
(1)對數列A:-2,2,-1,1,3,寫出G(A)的所有元素;
(2)證明:若數列A中存在 ![]() 使得
使得 ![]() >
> ![]() ,則G(A)
,則G(A) ![]()
![]() ;
;
(3)證明:若數列A滿足 ![]() -
- ![]() ≤1(n=2,3, …,N),則GA.的元素個數不小于
≤1(n=2,3, …,N),則GA.的元素個數不小于 ![]() -
- ![]() 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A、B是單位圓O上的兩點(O為圓心),∠AOB=120°,點C是線段AB上不與A、B重合的動點.MN是圓O的一條直徑,則![]() 的取值范圍是( )
的取值范圍是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選做題】本題包括A、B、C、D四小題,請選定其中兩小題,并在相應的答題區域內作答.若多做,則按作答的前兩小題評分.解答時應寫出文字說明、證明過程或演算步驟.
(1)A.【選修4—1幾何證明選講】
如圖,在△ABC中,∠ABC=90°,BD⊥AC , D為垂足,E是BC的中點,求證:∠EDC=∠ABD.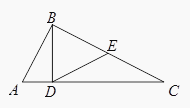
(2)B.【選修4—2:矩陣與變換】
已知矩陣A= ![]() 矩陣B的逆矩陣B﹣1=
矩陣B的逆矩陣B﹣1= 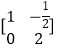 ,求矩陣AB.
,求矩陣AB.
(3)【選修4—4:坐標系與參數方程】在平面直角坐標系xOy中,已知直線l的參數方程為 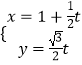 (t為參數),橢圓C的參數方程為
(t為參數),橢圓C的參數方程為 ![]() (
( ![]() 為參數).設直線l與橢圓C相交于A , B兩點,求線段AB的長.
為參數).設直線l與橢圓C相交于A , B兩點,求線段AB的長.
(4)D. 設a>0,|x﹣1|< ![]() ,|y﹣2|<
,|y﹣2|< ![]() ,求證:|2x+y﹣4|<a.
,求證:|2x+y﹣4|<a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某化工廠生產甲、乙兩種混合肥料,需要A,B,C三種主要原料,生產1扯皮甲種肥料和生產1車皮乙種肥料所需三種原料的噸數如表所示:
配料 原料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
現有A種原料200噸,B種原料360噸,C種原料300噸,在此基礎上生產甲、乙兩種肥料.已知生產1車皮甲種肥料,產生的利潤為2萬元;生產1車品乙種肥料,產生的利潤為3萬元、分別用x,y表示計劃生產甲、乙兩種肥料的車皮數.
(1)用x,y列出滿足生產條件的數學關系式,并畫出相應的平面區域;
(2)問分別生產甲、乙兩種肥料,求出此最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】漳州市博物館為了保護一件珍貴文物,需要在館內一種透明又密封的長方體玻璃保護罩內充入保護液體.該博物館需要支付的總費用由兩部分組成:①罩內該種液體的體積比保護罩的容積少0.5立方米,且每立方米液體費用500元;②需支付一定的保險費用,且支付的保險費用與保護罩容積成反比,當容積為2立方米時,支付的保險費用為4000元.
(Ⅰ)求該博物館支付總費用![]() 與保護罩容積
與保護罩容積![]() 之間的函數關系式;
之間的函數關系式;
(Ⅱ)求該博物館支付總費用的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】三棱錐被平行于底面ABC的平面所截得的幾何體如圖所示,截面為A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() .
.
(1)證明:BC![]() A1D;
A1D;
(2)求二面角A-CC1-B的余弦值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com