
【題目】已知定義在![]() 上的偶函數(shù)
上的偶函數(shù)![]() 滿足
滿足![]() ,且
,且![]() 時,
時,![]() ,則函數(shù)
,則函數(shù)![]() 在
在![]() 上的所有零點之和為( )
上的所有零點之和為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
把函數(shù)g(x)![]() f(x)﹣cosπx的零點轉(zhuǎn)化為兩函數(shù)y=f(x)與y=cosπx圖象交點的橫坐標(biāo),再由已知可得函數(shù)f(x)的對稱軸與周期,作出函數(shù)y=f(x)與y=cosπx的圖象,數(shù)形結(jié)合得答案.
f(x)﹣cosπx的零點轉(zhuǎn)化為兩函數(shù)y=f(x)與y=cosπx圖象交點的橫坐標(biāo),再由已知可得函數(shù)f(x)的對稱軸與周期,作出函數(shù)y=f(x)與y=cosπx的圖象,數(shù)形結(jié)合得答案.
函數(shù)g(x)![]() f(x)﹣cosπx的零點,即方程f(x)﹣cosπx=0的根,
f(x)﹣cosπx的零點,即方程f(x)﹣cosπx=0的根,
也就是兩函數(shù)y=f(x)與y=cosπx圖象交點的橫坐標(biāo).
由f(x)是定義在R上的偶函數(shù),且![]()
可得函數(shù)周期為2.
又當(dāng)![]() 時,
時,![]() ,
,
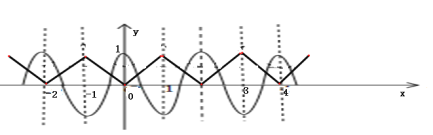
作出函數(shù)y=f(x)與y=cosπx的圖象如圖:
由圖可知,函數(shù)g(x)![]() f(x)﹣cosπx
f(x)﹣cosπx
在區(qū)間[﹣2,4]上的所有零點之和為﹣![]() 2+
2+![]() 2+
2+![]() 2=6.
2=6.
故選:C.


 習(xí)題精選系列答案
習(xí)題精選系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三實驗班的60名學(xué)生期中考試的語文、數(shù)學(xué)成績都在![]() 內(nèi),其中語文成績分組區(qū)間是:
內(nèi),其中語文成績分組區(qū)間是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .其成績的頻率分布直方圖如圖所示,這60名學(xué)生語文成績某些分?jǐn)?shù)段的人數(shù)
.其成績的頻率分布直方圖如圖所示,這60名學(xué)生語文成績某些分?jǐn)?shù)段的人數(shù)![]() 與數(shù)學(xué)成績相應(yīng)分?jǐn)?shù)段的人數(shù)
與數(shù)學(xué)成績相應(yīng)分?jǐn)?shù)段的人數(shù)![]() 之比如下表所示:
之比如下表所示:
分組區(qū)間 |
|
|
|
|
|
|
|
|
|
| |
24 | 3 | ||||
數(shù)學(xué)人數(shù) | 12 | 4 |
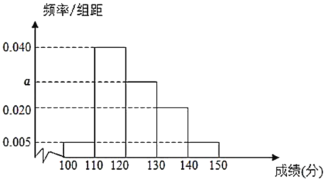
(1)求圖中![]() 的值及數(shù)學(xué)成績在
的值及數(shù)學(xué)成績在![]() 的人數(shù);
的人數(shù);
(2)語文成績在![]() 的3名學(xué)生均是女生,數(shù)學(xué)成績在
的3名學(xué)生均是女生,數(shù)學(xué)成績在![]() 的4名學(xué)生均是男生,現(xiàn)從這7名學(xué)生中隨機選取4名學(xué)生,事件
的4名學(xué)生均是男生,現(xiàn)從這7名學(xué)生中隨機選取4名學(xué)生,事件![]() 為:“其中男生人數(shù)不少于女生人數(shù)”,求事件
為:“其中男生人數(shù)不少于女生人數(shù)”,求事件![]() 發(fā)生的概率;
發(fā)生的概率;
(3)若從數(shù)學(xué)成績在![]() 的學(xué)生中隨機選取2名學(xué)生,且這2名學(xué)生中數(shù)學(xué)成績在
的學(xué)生中隨機選取2名學(xué)生,且這2名學(xué)生中數(shù)學(xué)成績在![]() 的人數(shù)為
的人數(shù)為![]() ,求
,求![]() 的分布列和數(shù)學(xué)期望
的分布列和數(shù)學(xué)期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司準(zhǔn)備投產(chǎn)一種新產(chǎn)品,經(jīng)測算,已知每年生產(chǎn)![]() 萬件的該種產(chǎn)品所需要的總成本
萬件的該種產(chǎn)品所需要的總成本![]() (萬元),依據(jù)產(chǎn)品尺寸,產(chǎn)品的品質(zhì)可能出現(xiàn)優(yōu)、中、差三種情況,隨機抽取了1000件產(chǎn)品測量尺寸,尺寸分別在
(萬元),依據(jù)產(chǎn)品尺寸,產(chǎn)品的品質(zhì)可能出現(xiàn)優(yōu)、中、差三種情況,隨機抽取了1000件產(chǎn)品測量尺寸,尺寸分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:
(單位:![]() )中,經(jīng)統(tǒng)計得到的頻率分布直方圖如圖所示.
)中,經(jīng)統(tǒng)計得到的頻率分布直方圖如圖所示.
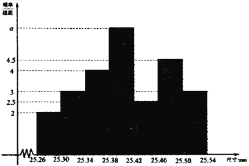
產(chǎn)品的品質(zhì)情況和相應(yīng)的價格![]() (元/件)與年產(chǎn)量
(元/件)與年產(chǎn)量![]() 之間的函數(shù)關(guān)系如下表所示.
之間的函數(shù)關(guān)系如下表所示.
產(chǎn)品品質(zhì) | 立品尺寸的范圍 | 價格 |
優(yōu) |
|
|
中 |
|
|
差 |
|
|
以頻率作為概率解決如下問題:
(1)求實數(shù)![]() 的值;
的值;
(2)當(dāng)產(chǎn)量![]() 確定時,設(shè)不同品質(zhì)的產(chǎn)品價格為隨機變量
確定時,設(shè)不同品質(zhì)的產(chǎn)品價格為隨機變量![]() ,求隨機變量
,求隨機變量![]() 的分布列;
的分布列;
(3)估計當(dāng)年產(chǎn)量![]() 為何值時,該公司年利潤最大,并求出最大值.
為何值時,該公司年利潤最大,并求出最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某紀(jì)念章從某年某月某日起開始上市,通過市場調(diào)査,得到該紀(jì)念章每![]() 枚的市場價
枚的市場價![]() (單位:元)與上市時間
(單位:元)與上市時間![]() (單位:天)的數(shù)據(jù)如下:
(單位:天)的數(shù)據(jù)如下:
上市時間 |
|
|
|
市場價 |
|
|
|
(1)根據(jù)上表數(shù)計,從下列函數(shù)中選取一個恰當(dāng)?shù)暮瘮?shù)描述該紀(jì)念章的市場價![]() 與上市時間
與上市時間![]() 的變化關(guān)系并說明理由:①
的變化關(guān)系并說明理由:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;
;
(2)利用你選取的函數(shù),求該紀(jì)念章市場價最低時的上市天數(shù)及最低的價格.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
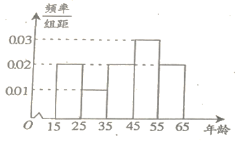
【題目】中央政府為了應(yīng)對因人口老齡化而造成的勞動力短缺等問題,擬定出臺“延遲退休年齡政策”.為了了解人們對“延遲退休年齡政策”的態(tài)度,責(zé)成人社部進行調(diào)研.人社部從網(wǎng)上年齡在15~65歲的人群中隨機調(diào)查100人,調(diào)查數(shù)據(jù)的頻率分布直方圖和支持“延遲退休”的人數(shù)與年齡的統(tǒng)計結(jié)果如下:
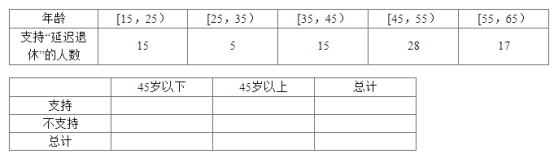
(1)由以上統(tǒng)計數(shù)據(jù)填2×2列聯(lián)表,并判斷能否在犯錯誤的概率不超過0.05的前提下認(rèn)為以45歲為分界點的不同人群對“延遲退休年齡政策”的支持度有差異;
(2)從調(diào)查的100人中年齡在15~25,25~35兩組按分層抽樣的方法抽取6人參加某項活動現(xiàn)從這6人中隨機抽2人,求這2人中至少1人的年齡在25~35之間的概率.
參考數(shù)據(jù):

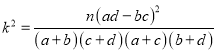 其中n=a+b+c+d
其中n=a+b+c+d
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.![]() ,且
,且![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 與函數(shù)
與函數(shù)![]() 在公共點
在公共點![]() 處有相同的切線,且
處有相同的切線,且![]() 在
在![]() 上恒成立.
上恒成立.
(i)求![]() 和
和![]() 的值;(
的值;(![]() 為函數(shù)
為函數(shù)![]() 的導(dǎo)函數(shù))
的導(dǎo)函數(shù))
(ii)求實數(shù)n的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某地區(qū)某種昆蟲產(chǎn)卵數(shù)和溫度有關(guān).現(xiàn)收集了一只該品種昆蟲的產(chǎn)卵數(shù)![]() (個)和溫度
(個)和溫度![]() (
(![]() )的7組觀測數(shù)據(jù),其散點圖如所示:
)的7組觀測數(shù)據(jù),其散點圖如所示:
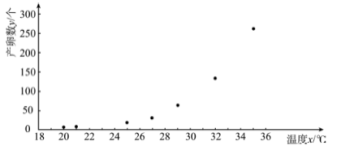
根據(jù)散點圖,結(jié)合函數(shù)知識,可以發(fā)現(xiàn)產(chǎn)卵數(shù)![]() 和溫度
和溫度![]() 可用方程
可用方程![]() 來擬合,令
來擬合,令![]() ,結(jié)合樣本數(shù)據(jù)可知
,結(jié)合樣本數(shù)據(jù)可知![]() 與溫度
與溫度![]() 可用線性回歸方程來擬合.根據(jù)收集到的數(shù)據(jù),計算得到如下值:
可用線性回歸方程來擬合.根據(jù)收集到的數(shù)據(jù),計算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和溫度
和溫度![]() 的回歸方程(回歸系數(shù)結(jié)果精確到
的回歸方程(回歸系數(shù)結(jié)果精確到![]() );
);
(2)求產(chǎn)卵數(shù)![]() 關(guān)于溫度
關(guān)于溫度![]() 的回歸方程;若該地區(qū)一段時間內(nèi)的氣溫在
的回歸方程;若該地區(qū)一段時間內(nèi)的氣溫在![]() 之間(包括
之間(包括![]() 與
與![]() ),估計該品種一只昆蟲的產(chǎn)卵數(shù)的范圍.(參考數(shù)據(jù):
),估計該品種一只昆蟲的產(chǎn)卵數(shù)的范圍.(參考數(shù)據(jù):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:對于一組數(shù)據(jù)![]() ,
,![]() ,…,
,…,![]() ,其回歸直線
,其回歸直線![]() 的斜率和截距的最小二乘估計分別為
的斜率和截距的最小二乘估計分別為 .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com