
【題目】截止到1999年底,我國人口約為13億,若今后能將人口平均增長率控制在1%,經過x年后,我國人口為y(單位:億).
(1)求y與x的函數關系式y=f(x);
(2)求函數y=f(x)的定義域;
(3)判斷函數f(x)是增函數還是減函數,并指出函數增減的實際意義.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析
;(3)見解析
【解析】試題分析:
(1)由題意對每年的人數進行求解,然后歸納可得函數的解析式為y=f(x)=13×(1+1%)x;
(2)結合實際問題的應用范圍可得函數的定義域為x∈N*;
(3)函數的底數大于1,則函數為增函數,其實際意義為只要遞增率為正數,隨著時間的推移,人口的總數總在增長.
試題解析:
(1)1999年底人口數:13億.經過1年,2000年底人口數:13+13×1%=13×(1+1%)億.經過2年,2001年底人口數:13×(1+1%)+13×(1+1%)×1%=13×(1+1%)2億.經過3年,2002年底人口數:13×(1+1%)2+13×(1+1%)2×1%=13×(1+1%)3億…
∵經過年數與(1+1%)的指數相同,∴經過x年后人口數為13×(1+1%)x億,∴y=f(x)=13×(1+1%)x.
(2)∵此問題以年作為單位時間,∴x∈N*是此函數的定義域.
(3)y=f(x)=13×(1+1%)x.∵1+1%>1,13>0,∴y=f(x)=13×(1+1%)x是增函數,
即只要遞增率為正數,隨著時間的推移,人口的總數總在增長.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2-2ax+2+b(a≠0)在區間[2,3]上有最大值5,最小值2.
(1)求a,b的值;
(2)若b<1,g(x)=f(x)-2mx在[2,4]上單調,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,下圖![]() 為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含
為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含![]() 個小正方形.
個小正方形.

(1)求出![]() ;
;
(2)利用合情推理的“歸納推理思想”歸納出![]() 與
與![]() 的關系式,
的關系式,
(3)根據你得到的關系式求![]() 的表達式
的表達式
查看答案和解析>>
科目:高中數學 來源: 題型:
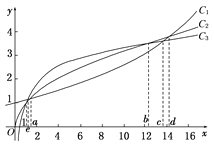
【題目】函數f(x)=1.1x,g(x)=ln x+1,h(x)=x![]() 的圖象如圖所示,試分別指出各曲線對應的函數,并比較三個函數的增長差異(以1,a,b,c,d,e為分界點).
的圖象如圖所示,試分別指出各曲線對應的函數,并比較三個函數的增長差異(以1,a,b,c,d,e為分界點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝![]() 臺發電機的水電站,過去
臺發電機的水電站,過去![]() 年的水文資料顯示,水庫年入流量
年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和.單位:億立方米)都在40以上,不足
(年入流量:一年內上游來水與庫區降水之和.單位:億立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超過
且不超過![]() 的年份有
的年份有![]() 年,超過
年,超過![]() 的年份有
的年份有![]() 年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
年,將年入流量在以上三段的頻率作為相應段的概率,假設各年的年入流量相互獨立.
(1)求未來![]() 年中,設
年中,設![]() 表示流量超過
表示流量超過![]() 的年數,求
的年數,求![]() 的分布列及期望;
的分布列及期望;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 限制,并有如下關系:
限制,并有如下關系:
年入流量 |
|
|
|
發電機最多可運行臺數 |
|
|
|
若某臺發電機運行,則該臺年利潤為![]() 萬元,若某臺發電機未運行,則該臺年虧損
萬元,若某臺發電機未運行,則該臺年虧損![]() 萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
萬元,欲使水電站年總利潤的均值達到最大,應安裝發電機多少臺?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線y=Asin(ωx+φ)(A>0,ω>0)上的一個最高點的坐標為(![]() ,
,![]() ),由此點到相鄰最低點間的曲線與x軸交于點(
),由此點到相鄰最低點間的曲線與x軸交于點(![]() π,0),φ∈(﹣
π,0),φ∈(﹣![]() ,
,![]() ).
).
(1)求這條曲線的函數解析式;
(2)寫出函數的單調區間.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com