
已知函數(shù)![]() ,
,
(Ⅰ)若![]() 是函數(shù)
是函數(shù)![]() 的一個(gè)極值點(diǎn),求實(shí)數(shù)
的一個(gè)極值點(diǎn),求實(shí)數(shù)![]() 的值;
的值;
(Ⅱ)設(shè)![]() ,當(dāng)
,當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的圖象恒不在直線
的圖象恒不在直線![]() 上方,求實(shí)數(shù)
上方,求實(shí)數(shù)![]() 的取值范圍。
的取值范圍。
解析:(1)由![]() 可得
可得
![]()
![]()
∵![]() 是函數(shù)
是函數(shù)![]() 的一個(gè)極值點(diǎn),∴
的一個(gè)極值點(diǎn),∴![]()
∴![]() , 解得
, 解得![]()
代入![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,當(dāng)
,當(dāng)![]() 時(shí),
時(shí),![]()
可知![]() 是函數(shù)
是函數(shù)![]() 的一個(gè)極值點(diǎn)。 ∴
的一個(gè)極值點(diǎn)。 ∴![]()
(2)要![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 的圖象恒不在直線
的圖象恒不在直線![]() 上方,
上方,
即![]() 時(shí),
時(shí),![]() 恒成立,
恒成立,
只要![]() 時(shí),
時(shí),![]() 成立
成立
由(1)知![]() ,令
,令![]() ,解得
,解得![]()
當(dāng)![]() 時(shí),
時(shí),![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() ,
,![]() 與
與![]() 矛盾,舍去
矛盾,舍去
當(dāng)![]() 時(shí),
時(shí),![]() ,
,
![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增
上單調(diào)遞增
∴![]() 在
在![]() 或
或![]() 處取到
處取到![]()
∴只要![]() ,解得
,解得![]()
當(dāng)![]() 時(shí),
時(shí),![]() ,∴
,∴![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
![]() 符合題意
符合題意


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源:2013-2014學(xué)年上海市長寧區(qū)高三上學(xué)期教學(xué)質(zhì)量檢測理科數(shù)學(xué)試卷(解析版) 題型:解答題
已知函數(shù) ,
,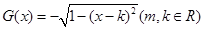
(1)若 是常數(shù),問當(dāng)
是常數(shù),問當(dāng) 滿足什么條件時(shí),函數(shù)
滿足什么條件時(shí),函數(shù) 有最大值,并求出
有最大值,并求出 取最大值時(shí)
取最大值時(shí) 的值;
的值;
(2)是否存在實(shí)數(shù)對 同時(shí)滿足條件:(甲)
同時(shí)滿足條件:(甲) 取最大值時(shí)
取最大值時(shí) 的值與
的值與 取最小值的
取最小值的 值相同,(乙)
值相同,(乙) ?
?
(3)把滿足條件(甲)的實(shí)數(shù)對 的集合記作A,設(shè)
的集合記作A,設(shè) ,求使
,求使 的
的 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012屆山西大學(xué)附中高三4月月考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分12分)已知函數(shù) ,其中
,其中 .
.
(Ⅰ)若 是
是 的極值點(diǎn),求
的極值點(diǎn),求 的值;
的值;
(Ⅱ)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若 在
在 上的最大值是
上的最大值是 ,求
,求 的取值范圍 .
的取值范圍 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013屆安徽省蚌埠市高二下學(xué)期期中聯(lián)考理科數(shù)學(xué)試卷(解析版) 題型:解答題
(本題滿分12分)
已知函數(shù) ,
,
(1)若 是
是 的極值點(diǎn),求
的極值點(diǎn),求 值;
值;
(2)若函數(shù) 在
在 上是增函數(shù),求實(shí)數(shù)
上是增函數(shù),求實(shí)數(shù) 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年甘肅省高三第二次診斷性考試?yán)砜茢?shù)學(xué)試卷 題型:解答題
(本小題滿分14分)已知函數(shù) ,其中
,其中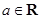 .
.
(Ⅰ)若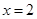 是
是 的極值點(diǎn),求
的極值點(diǎn),求 的值;
的值;
(Ⅱ)求 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若 在
在 上的最大值是
上的最大值是 ,求
,求 的取值范圍)
的取值范圍)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2011-2012學(xué)年四川省高三2月月考理科數(shù)學(xué) 題型:解答題
已知函數(shù) ,其中
,其中 .
.
(Ⅰ)若 是
是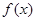 的極值點(diǎn),求
的極值點(diǎn),求 的值;
的值;
(Ⅱ)求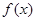 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅲ)若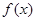 在
在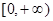 上的最大值是
上的最大值是 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com