
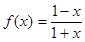 .滿足
.滿足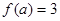 ,則
,則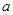 的值為( )
的值為( )A.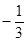 | B.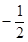 | C.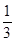 | D.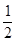 |
 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:高中數(shù)學 來源:不詳 題型:解答題
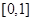 上的函數(shù)
上的函數(shù)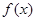 同時滿足:①
同時滿足:①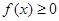 ;②
;②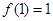 ;③若
;③若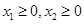 ,且
,且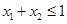 ,則
,則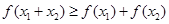 成立.則稱函數(shù)
成立.則稱函數(shù)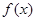 為“夢函數(shù)”.
為“夢函數(shù)”. 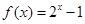 在區(qū)間
在區(qū)間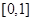 上是否為“夢函數(shù)”;
上是否為“夢函數(shù)”;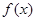 為“夢函數(shù)”,求
為“夢函數(shù)”,求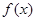 的最值.
的最值.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
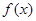 的圖象恰好通過
的圖象恰好通過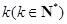 個格點,則稱函數(shù)
個格點,則稱函數(shù)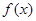 為
為 階格點函數(shù). 給出下列4個函數(shù):
階格點函數(shù). 給出下列4個函數(shù):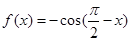 ;②
;②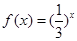 ;③
;③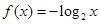 ;④
;④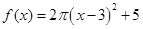 .
.| A.①③ | B.②③ | C.③④ | D.①④ |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 年(
年( 為正整數(shù),2012年為第一年)的利潤為
為正整數(shù),2012年為第一年)的利潤為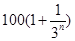 萬元.設從2012年起的前
萬元.設從2012年起的前 年,該廠不開發(fā)新項目的累計利潤為
年,該廠不開發(fā)新項目的累計利潤為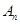 萬元,開發(fā)新項目的累計利潤為
萬元,開發(fā)新項目的累計利潤為 萬元(須扣除開發(fā)所投入資金).
萬元(須扣除開發(fā)所投入資金). ,
, 的表達式;
的表達式;查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
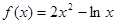 在其定義域內的一個子區(qū)間(k-1,k+1)內不是單調函數(shù),則實數(shù)k的取值范圍是( )
在其定義域內的一個子區(qū)間(k-1,k+1)內不是單調函數(shù),則實數(shù)k的取值范圍是( )A.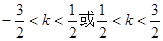 | B.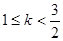 |
C.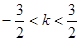 | D.不存在這樣的實數(shù)k |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 ,曲線
,曲線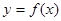 在點
在點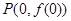 處的切線方程為
處的切線方程為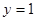
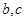 的值
的值 的三條不同切線,求
的三條不同切線,求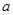 的取值范圍
的取值范圍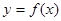 在點
在點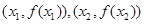 處的切線都過點(0,2),證明:當
處的切線都過點(0,2),證明:當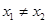 時,
時,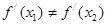
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
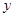 (萬元)隨投資收益
(萬元)隨投資收益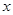 (萬元)的增加而增加,但獎金總數(shù)不超過9萬元,同時獎金不超過投資收益的20%.
(萬元)的增加而增加,但獎金總數(shù)不超過9萬元,同時獎金不超過投資收益的20%. 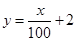 ;②
;②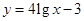 .
.查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
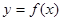 是定義在
是定義在 上的奇函數(shù),且當
上的奇函數(shù),且當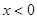 時,不等式
時,不等式 成立,若
成立,若 ,
, ,
,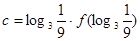 ,則a,b,c間的大小關系是( ).
,則a,b,c間的大小關系是( ).| A.a(chǎn)>b>c | B.c>b>a | C.c>a>b | D.a(chǎn)>c>b |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com