
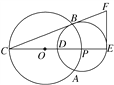
【題目】如圖,圓O與圓P相交于A,B兩點,圓心P在圓O上,圓O的弦BC切圓P于點B,CP及其延長線交圓P于D,E兩點,過點E作EF⊥CE,交CB的延長線于點F.
(1)求證:B,P,E,F四點共圓;
(2)若CD=2,CB=2![]() ,求出由B,P,E,F四點所確定的圓的直徑.
,求出由B,P,E,F四點所確定的圓的直徑.
【答案】(1)見解析(2) ![]()
【解析】試題分析:(1)欲證四點B、P、E、F共圓,只要通過三角形Rt△CBP和Rt△CEF相似證明由此四點構成的四邊形對角互補即可;
(2)先根據(1)中四點B,P,E,F共圓條件得切線,再由切割線定理及三角形相似求得EF,最后再結合勾股定理求得PF即為所求圓的直徑即可.
試題解析:
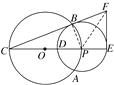
(1)證明:如圖,連接PB.
因為BC切圓P于點B,所以PB⊥BC.
 因為EF⊥CE,所以∠PBF+∠PEF=180°,
因為EF⊥CE,所以∠PBF+∠PEF=180°,
所以B,P,E,F四點共圓.
(2)連接PF,因為B,P,E,F四點共圓,
且EF⊥CE,PB⊥BC,所以此圓的直徑就是PF.
因為BC切圓P于點B,且CD=2,CB=2![]() ,
,
所以由切割線定理得CB2=CD·CE,
所以CE=4,所以DE=2,則BP=PE=1.
又因為Rt△CBP ∽Rt△CEF,
所以![]() =
=![]() ,得EF=
,得EF=![]() .
.
在Rt△FEP中,PF=![]() =
=![]() ,
,
即由B,P,E,F四點確定的圓的直徑為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知m∈R,復數z= ![]() +(m2+2m﹣3)i,當m為何值時,
+(m2+2m﹣3)i,當m為何值時,
(1)z∈R;
(2)z是純虛數;
(3)z對應的點位于復平面第二象限;
(4)(選做)z對應的點在直線x+y+3=0上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記所有非零向量構成的集合為V,對于 ![]() ,
, ![]() ∈V,
∈V, ![]() ≠
≠ ![]() ,定義V(
,定義V( ![]() ,
, ![]() )=|x∈V|x
)=|x∈V|x ![]() =x
=x ![]() |
|
(1)請你任意寫出兩個平面向量 ![]() ,
, ![]() ,并寫出集合V(
,并寫出集合V( ![]() ,
, ![]() )中的三個元素;
)中的三個元素;
(2)請根據你在(1)中寫出的三個元素,猜想集合V( ![]() ,
, ![]() )中元素的關系,并試著給出證明;
)中元素的關系,并試著給出證明;
(3)若V( ![]() ,
, ![]() )=V(
)=V( ![]() ,
, ![]() ),其中
),其中 ![]() ≠
≠ ![]() ,求證:一定存在實數λ1 , λ2 , 且λ1+λ2=1,使得
,求證:一定存在實數λ1 , λ2 , 且λ1+λ2=1,使得 ![]() =λ1
=λ1 ![]() +λ2
+λ2 ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
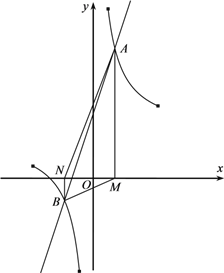
【題目】如圖,已知直線![]() 與曲線
與曲線![]() 在第一象限和第三象限分別交于點
在第一象限和第三象限分別交于點![]() 和點
和點![]() ,分別由點
,分別由點![]() 、
、![]() 向
向![]() 軸作垂線,垂足分別為
軸作垂線,垂足分別為![]() 、
、![]() ,記四邊形
,記四邊形![]() 的面積為S.
的面積為S.
⑴ 求出點![]() 、
、![]() 的坐標及實數
的坐標及實數![]() 的取值范圍;
的取值范圍;
⑵ 當![]() 取何值時,S取得最小值,并求出S的最小值.
取何值時,S取得最小值,并求出S的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對某電子元件進行壽命追蹤調查,情況如下.
壽命(h) | 100~200 | 200~300 | 300~400 | 400~500 | 500~600 |
個 數 | 20 | 30 | 80 | 40 | 30 |
(1)列出頻率分布表;
(2)畫出頻率分布直方圖;
(3)估計元件壽命在100~400h以內的在總體中占的比例.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=sin2x+2 ![]() cos2x﹣
cos2x﹣ ![]() ,函數g(x)=mcos(2x﹣
,函數g(x)=mcos(2x﹣ ![]() )﹣2m+3(m>0),若存在x1 , x2∈[0,
)﹣2m+3(m>0),若存在x1 , x2∈[0, ![]() ],使得f(x1)=g(x2)成立,則實數m的取值范圍是( )
],使得f(x1)=g(x2)成立,則實數m的取值范圍是( )
A.(0,1]
B.[1,2]
C.[ ![]() ,2]
,2]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次數學測驗中,有6位同學的平均成績為117分,用![]() 表示編號為
表示編號為![]() 的同學所得成 績,6位同學成績如表,
的同學所得成 績,6位同學成績如表,

(1)求![]() 及這6位同學成績的方差;
及這6位同學成績的方差;
(2)從這6位同學中隨機選出2位同學,則恰有1位同學成績在區間![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某廠家舉行大型的促銷活動,經測算某產品當促銷費用為![]() 萬元時,銷售量
萬元時,銷售量![]() 萬件滿足
萬件滿足![]() (其中
(其中![]() ,
, ![]() 為正常數),現假定生產量與銷售量相等,已知生產該產品
為正常數),現假定生產量與銷售量相等,已知生產該產品![]() 萬件還需投入成本
萬件還需投入成本![]() 萬元(不含促銷費用),產品的銷售價格定為
萬元(不含促銷費用),產品的銷售價格定為![]() 萬元/萬件.
萬元/萬件.
(1)將該產品的利潤![]() 萬元表示為促銷費用
萬元表示為促銷費用![]() 萬元的函數;
萬元的函數;
(2)促銷費用投入多少萬元時,廠家的利潤最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com