
【題目】已知函數![]() ,且
,且![]() .
.
(1)求函數![]() 的極值;
的極值;
(2)當![]() 時,證明:
時,證明: .
.
【答案】(1)當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,當
,當![]() 時,函數
時,函數![]() 有極小值
有極小值![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
試題分析:(1)求極值,可先求得導數![]() ,然后通過解不等式
,然后通過解不等式![]() 確定增區間,解不等式
確定增區間,解不等式![]() 確定減區間,則可得極大值和極小值;(2)要證明此不等式,我們首先研究不等式左邊的函數,記
確定減區間,則可得極大值和極小值;(2)要證明此不等式,我們首先研究不等式左邊的函數,記![]() ,求出其導數
,求出其導數![]() ,可知
,可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,![]() ,這是
,這是![]() 時最小值,
時最小值,![]() ,這是
,這是![]() 時的最大值,因此要證明題中不等式,可分類,
時的最大值,因此要證明題中不等式,可分類,![]() 和
和![]() 分別證明.
分別證明.
試題解析:(1)依題意,![]() ,
,
故![]() ,
,
令![]() ,則
,則![]() 或
或![]() ; 令
; 令![]() ,則
,則![]() ,
,
故當![]() 時,函數
時,函數![]() 有極大值
有極大值![]() ,當
,當![]() 時,函數
時,函數![]() 有極小值
有極小值![]() .
.
(2) 由(1)知![]() ,令
,令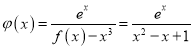 ,
,
則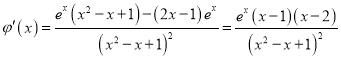 ,
,
可知![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,令
上單調遞減,令![]() .
.
① 當![]() 時,
時,![]() ,所以函數
,所以函數![]() 的圖象在
的圖象在![]() 圖象的上方.
圖象的上方.
② 當![]() 時,函數
時,函數![]() 單調遞減,所以其最小值為
單調遞減,所以其最小值為![]() 最大值為2,而
最大值為2,而![]() ,所以函數
,所以函數![]() 的圖象也在
的圖象也在![]() 圖象的上方.
圖象的上方.
綜上可知,當![]() 時,
時,


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】給出下列關系:其中具有相關關系的是( )
①考試號與考生考試成績; ②勤能補拙;
③水稻產量與氣候; ④正方形的邊長與正方形的面積.
A.①②③B.①③④C.②③D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知首項為![]() 的正項數列
的正項數列![]() 滿足
滿足![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)設數列![]() 是公比為
是公比為![]() 的等比數列,
的等比數列,![]() 為數列
為數列![]() 前
前![]() 項的和.若
項的和.若![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() )成等差數列,且
)成等差數列,且![]() ,求正整數
,求正整數![]() 的最小值,以及
的最小值,以及![]() 取最小值時相應數列
取最小值時相應數列![]() ,
,![]() ,
,![]() ,
,![]() 的公差.
的公差.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學的父親決定今年夏天賣西瓜賺錢,根據去年6月份的數據統計連續五天內每天所賣西瓜的個數與溫度之間的關系如下表:
溫度 | 32 | 33 | 35 | 37 | 38 |
西瓜個數 | 20 | 22 | 24 | 30 | 34 |
(1)求這五天內所賣西瓜個數的平均值和方差;
(2)求變量![]() 之間的線性回歸方程,并預測當溫度為
之間的線性回歸方程,并預測當溫度為![]() 時所賣西瓜的個數.
時所賣西瓜的個數.
附: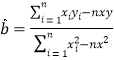 ,
,![]() (精確到
(精確到![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 已知函數![]() (
(![]() ,
,![]() )的圖像關于直線x=
)的圖像關于直線x=![]() 對稱,最大值為3,且圖像上相鄰兩個最高點的距離為
對稱,最大值為3,且圖像上相鄰兩個最高點的距離為![]() .
.
(1)求![]() 的最小正周期;
的最小正周期;
(2)求函數![]() 的解析式;
的解析式;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax-![]() -5ln x,g(x)=x2-mx+4.
-5ln x,g(x)=x2-mx+4.
(1)若x=2是函數f(x)的極值點,求a的值;
(2)當a=2時,若x1∈(0,1),x2∈[1,2],都有f(x1)≥g(x2)成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:關于x的不等式ax>1(a>0,a≠1)的解集是{x|x<0},命題q:函數y=lg(ax2-x+a)的定義域為R,如果p∨q為真命題,p∧q為假命題,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com