
【題目】某單位有工程師6人,技術員12人,技工18人,要從這些人中取一個容量為n的樣本;如果采用系統抽樣和分層抽樣方法抽取,無須剔除個體;如果樣本容量增加1個,則在采用系統抽樣時需要在總體中先剔除一個個體,則n的值為 .
【答案】6
【解析】解:由題意知采用系統抽樣和分層抽樣方法抽取,不用剔除個體;
如果樣本容量增加一個,則在采用系統抽樣時,
需要在總體中先剔除1個個體,
∵總體容量為6+12+18=36.
當樣本容量是n時,由題意知,系統抽樣的間隔為 ![]() ,
,
分層抽樣的比例是 ![]() ,抽取的工程師人數為
,抽取的工程師人數為 ![]() 6=
6= ![]() ,
,
技術員人數為 ![]() 12=
12= ![]() ,技工人數為
,技工人數為 ![]() 18=
18= ![]() ,
,
∵n應是6的倍數,36的約數,
即n=6,12,18.
當樣本容量為(n+1)時,總體容量是35人,
系統抽樣的間隔為 ![]() ,
,
∵ ![]() 必須是整數,
必須是整數,
∴n只能取6.
即樣本容量n=6.
所以答案是:6.
【考點精析】解答此題的關鍵在于理解分層抽樣的相關知識,掌握先將總體中的所有單位按照某種特征或標志(性別、年齡等)劃分成若干類型或層次,然后再在各個類型或層次中采用簡單隨機抽樣或系用抽樣的辦法抽取一個子樣本,最后,將這些子樣本合起來構成總體的樣本,以及對系統抽樣方法的理解,了解把總體的單位進行排序,再計算出抽樣距離,然后按照這一固定的抽樣距離抽取樣本;第一個樣本采用簡單隨機抽樣的辦法抽取.


科目:高中數學 來源: 題型:
【題目】已知直線: ![]() (
(![]() 為給定的正常數,
為給定的正常數, ![]() 為參數,
為參數, ![]() )構成的集合為
)構成的集合為![]() ,給出下列命題:
,給出下列命題:
①當![]() 時,
時, ![]() 中直線的斜率為
中直線的斜率為![]() ;
;
②![]() 中的所有直線可覆蓋整個坐標平面.
中的所有直線可覆蓋整個坐標平面.
③當![]() 時,存在某個定點,該定點到
時,存在某個定點,該定點到![]() 中的所有直線的距離均相等;
中的所有直線的距離均相等;
④當![]() 時,
時, ![]() 中的兩條平行直線間的距離的最小值為
中的兩條平行直線間的距離的最小值為![]() ;
;
其中正確的是__________(寫出所有正確命題的編號).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 點在底面
點在底面![]() 內的射影
內的射影![]() 在線段
在線段![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 在線段
在線段![]() 上,且
上,且![]() .
.
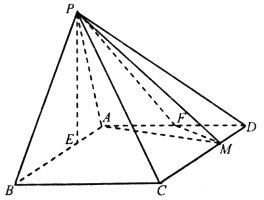
(Ⅰ)當![]() 時,證明:平面
時,證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)當平面![]() 與平面
與平面![]() 所成的二面角的正弦值為
所成的二面角的正弦值為![]() 時,求四棱錐
時,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】樣本a1 , a2 , a3 , …,a10的平均數為 ![]() ,樣本b1 , b2 , b3 , …,b10的平均數為
,樣本b1 , b2 , b3 , …,b10的平均數為 ![]() ,那么樣本a1 , b1 , a2 , b2 , …,a10 , b10的平均數為( )
,那么樣本a1 , b1 , a2 , b2 , …,a10 , b10的平均數為( )
A.![]() +
+ ![]()
![]()
B.![]() (
( ![]() +
+ ![]() )
)![]()
C.2( ![]() +
+ ![]() )
)
D.![]() (
( ![]() +
+ ![]() )
)![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題:
①函數 ![]() 是奇函數;
是奇函數;
②存在實數x,使sinx+cosx=2;
③若α,β是第一象限角且α<β,則tanα<tanβ;
④ ![]() 是函數
是函數 ![]() 的一條對稱軸;
的一條對稱軸;
⑤函數 ![]() 的圖象關于點
的圖象關于點 ![]() 成中心對稱.
成中心對稱.
其中正確命題的序號為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分圖象如圖所示,P、Q 分別為該圖象的最高點和最低點,點P的坐標為(1,A).點R的坐標為(1,0),∠PRQ=
.y=f(x)的部分圖象如圖所示,P、Q 分別為該圖象的最高點和最低點,點P的坐標為(1,A).點R的坐標為(1,0),∠PRQ= ![]() .
. 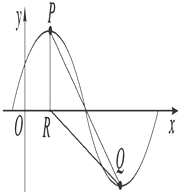
(1)求f(x)的最小正周期以及解析式.
(2)用五點法畫出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的圖象.
]上的圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】咖啡館配制兩種飲料,甲種飲料分別用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙種飲料分別用奶粉
。乙種飲料分別用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限額為奶粉
。已知每天使用原料限額為奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲種飲料每杯能獲利
。如果甲種飲料每杯能獲利![]() 元,乙種飲料每杯能獲利
元,乙種飲料每杯能獲利![]() 元。每天在原料的使用限額內飲料能全部售出,每天應配制兩種飲料各多少杯能獲利最大?
元。每天在原料的使用限額內飲料能全部售出,每天應配制兩種飲料各多少杯能獲利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列五個命題:①“若![]() ,則
,則![]() 或
或![]() ”是假命題;②從正方體的面對角線中任取兩條作為一對,其中所成角為
”是假命題;②從正方體的面對角線中任取兩條作為一對,其中所成角為![]() 的有48對;③“
的有48對;③“ ![]() ”是方程
”是方程![]() 表示焦點在
表示焦點在![]() 軸上的雙曲線的充分不必要條件;④點
軸上的雙曲線的充分不必要條件;④點![]() 是曲線
是曲線![]() (
(![]() ,
, ![]() )上的動點,且滿足
)上的動點,且滿足![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]() ;⑤若隨機變量
;⑤若隨機變量![]() 服從正態分布
服從正態分布![]() ,且
,且![]() ,則
,則![]() .其中正確命題的序號是__________(請把正確命題的序號填在橫線上).
.其中正確命題的序號是__________(請把正確命題的序號填在橫線上).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com