【題目】某工廠在生產產品時需要用到長度為
的
型和長度為
的
型兩種鋼管.工廠利用長度為
的鋼管原材料，裁剪成若干型和型鋼管，假設裁剪時損耗忽略不計，裁剪后所剩廢料與原材料的百分比稱為廢料率.
（1）要使裁剪的廢料率小于
，共有幾種方案剪裁？請寫出每種方案中分別被裁剪型鋼管和型鋼管的根數；
（2）假設一根型鋼管和一根型鋼管能成為一套毛胚，假定只能按（1）中的那些方案裁剪，若工廠需要生產
套毛胚，則至少需要采購多少根長度為的鋼管原材料？最終的廢料率為多少？
【答案】（1）見解析（2）見解析
【解析】
（1）設每根原材料可裁剪a根A型和b根B型鋼管，則
，再由廢料率小于
得
故
即可設計方案，（2）設用方案一裁剪x根原材料，用方案二裁剪y根原材料，共裁剪得z套毛胚，則
z＝2x+4y，由
得
即可求出答案．
（1）設每根原料可裁剪成
根
型鋼管和b根
型鋼管，則.
根據題意，廢料率為
故
滿足條件的a與b的值為
方案一：
廢料率為
；則可裁剪成2根A型鋼管和5根B型鋼管.
方案二：
廢料率為
.則可裁剪成4根A型鋼管和2根B型鋼管.
（2）設用方案一裁剪
根原材料，用方案二裁剪
根原材料，共裁剪得
套毛坯，則
,即
，故由題
，所以
所以至少采購100根長度為4000mm的鋼管原材料，其中方案一裁剪40根，方案二裁剪60根，廢料率為
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知某超市2018年12個月的收入與支出數據的折線圖如圖所示：
根據該折線圖可知，下列說法錯誤的是（ ）
A. 該超市2018年的12個月中的7月份的收益最高
B. 該超市2018年的12個月中的4月份的收益最低
C. 該超市2018年1-6月份的總收益低于2018年7-12月份的總收益
D. 該超市2018年7-12月份的總收益比2018年1-6月份的總收益增長了90萬元
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，四棱錐
中，
底面
，面是直角梯形，
為側棱
上一點．該四棱錐的俯視圖和側（左）視圖如圖2所示．
（1）證明：
平面
；
（2）線段
上是否存在點
，使
與
所成角的余弦值為
？若存在，找到所有符合要求的點，并求
的長；若不存在，說明理由．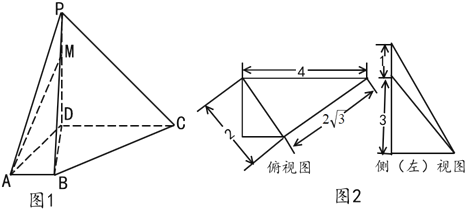
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】假設某種設備使用的年限
（年）與所支出的維修費用
（萬元）有以下統計資料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
維修費用 | 2 | 4 | 5 | 6 | 7 |
若由資料知對呈線性相關關系.試求：
（1）求
；
（2）線性回歸方程
；
（3）估計使用10年時，維修費用是多少？
附：利用“最小二乘法”計算
的值時，可根據以下公式：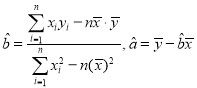
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
，若數列
滿足：對所有
，
，且當
時，
，則稱為“
數列”，設
R，函數
，數列
滿足
，
（
）.
（1）若
，而是
數列，求
的值；
（2）設
，證明：存在，使得是
數列，但對任意，都不是
數列；
（3）設
，證明：對任意，都存在，使得是數列.
查看答案和解析>>
科目：高中數學 來源： 題型：
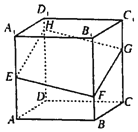
【題目】如圖，正方體
的棱長為
，作平面
與底面不平行
與棱
，
，
，
分別交于E，F，G，H，記EA，FB，GC，HD分別為
，
，
，
，若
，
，則多面體EFGHABCD的體積為
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，圓C的參數方程為
為參數
以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，直線的極坐標方程為
，且圓心C在直線l上．
Ⅰ
求直線l的直角坐標方程及圓C的極坐標方程；
Ⅱ若
是直線l上一點，
是圓C上一點，求
的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列
中的項按順序可以排列成如圖的形式，第一行
項，排
；第二行
項，從左到右分別排
，
；第三行
項，……以此類推，設數列的前
項和為
，則滿足
的最小正整數的值為（ ）
4,
4,4
3
4,43,4 
4,43,4 , 4 
…
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓的中心是坐標原點
，它的短軸長為
，一個焦點為
，一個定點
，且
，過點
的直線與橢圓相交于兩點
.
.
（1）求橢圓的方程及離心率.
（2）如果以
為直徑的圓過原點，求直線
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com