
 如圖所示:m個實a1a2…,am(m≥3且m∈N)依次按順時針方向圍成一個圓圈.
如圖所示:m個實a1a2…,am(m≥3且m∈N)依次按順時針方向圍成一個圓圈.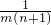 (n∈N,n<m),若am>1.99恒成立,求m的最小值;
(n∈N,n<m),若am>1.99恒成立,求m的最小值;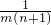 (n∈N,n<m),
(n∈N,n<m),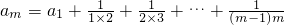
 +
+ -
- +…+
+…+ =2-
=2- ,
,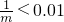 ,∴m>100,
,∴m>100, ,
,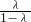 )m-2,又
)m-2,又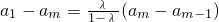 ,
,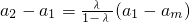 ,
,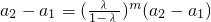 ,
,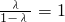 ,或a2-a1=0.
,或a2-a1=0.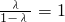 ,則
,則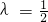 ,
,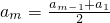 ,∴d=0,
,∴d=0,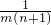 (n∈N,n<m),推導出am=2-
(n∈N,n<m),推導出am=2- ,由此能求出m的最小值.
,由此能求出m的最小值. ,由此利用分類討論思想能夠證明a1=a2=…=am.
,由此利用分類討論思想能夠證明a1=a2=…=am.

科目:高中數學 來源: 題型:
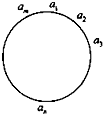 如圖所示:m個實a1a2…,am(m≥3且m∈N)依次按順時針方向圍成一個圓圈.
如圖所示:m個實a1a2…,am(m≥3且m∈N)依次按順時針方向圍成一個圓圈.| 1 | m(n+1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com