
【題目】如圖,在平面直角坐標系![]() 中,已知
中,已知![]() 分別是橢圓
分別是橢圓![]() :
:![]() (
(![]() )的左右焦點,點
)的左右焦點,點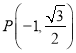 是橢圓
是橢圓![]() 上一點,且
上一點,且![]() .若橢圓
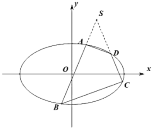
.若橢圓![]() 的內接四邊形
的內接四邊形![]() 的邊
的邊![]() 的延長線交于橢圓外一點
的延長線交于橢圓外一點![]() ,且點
,且點![]() 的橫坐標為1,記直線
的橫坐標為1,記直線![]() 的斜率分別為
的斜率分別為![]() ,
,![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)求橢圓定義可知![]() ,點
,點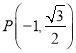 代入即可得出結果;
代入即可得出結果;
(2)設![]() ,
,![]() ,因為
,因為![]() 的延長線交于橢圓外一點
的延長線交于橢圓外一點![]() ,且點
,且點![]() 的橫坐標為1,于是有
的橫坐標為1,于是有![]() ,將直線與橢圓方程聯立,結合韋達定理及弦長公式可求得
,將直線與橢圓方程聯立,結合韋達定理及弦長公式可求得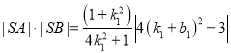 ,
,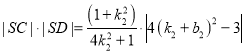 ,根據已知條件
,根據已知條件![]() 化簡即可得出結果.
化簡即可得出結果.
(1)![]()
![]() ,∴
,∴![]()
點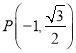 是橢圓
是橢圓![]() 上一點,代入方程:
上一點,代入方程:![]() ,∴
,∴![]() ,
,
∴橢圓![]() 的標準方程:
的標準方程:![]()
(2)設![]() ,
,![]()
![]() 的延長線交于橢圓外一點
的延長線交于橢圓外一點![]() ,且點
,且點![]() 的橫坐標為1,于是有
的橫坐標為1,于是有![]() ①
①
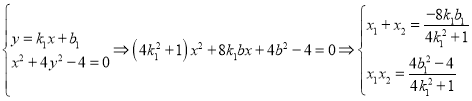 ②
②
于是:![]()
代入②可得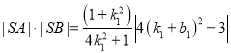
同理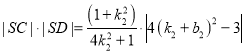
又![]() ,
,![]() 可得:
可得:![]()
∴![]()
法二:(1)由![]() 為橢圓
為橢圓![]() 的左右焦點,
的左右焦點,![]() 為
為![]() 上一點,
上一點,![]()
∴![]() ,∴
,∴![]() ,∴橢圓
,∴橢圓![]()
將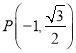 代入可得
代入可得![]()
∴橢圓![]() 的標準方程為
的標準方程為![]()
(2)設![]() ,由
,由![]() 斜率分別為
斜率分別為![]()
則直線![]() 的方程分別為
的方程分別為![]()
將![]() 與
與![]() 聯立,設
聯立,設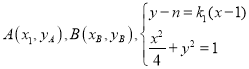
![]()
由韋達定理,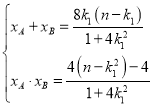
∴![]()
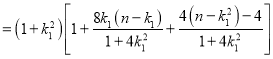
![]()
![]()
同理可證![]()
則由![]() ,得
,得![]()
從而![]()
即![]()
∴![]() ,∴
,∴![]()
又![]() 為
為![]() 的內接四邊形,∴
的內接四邊形,∴![]() ,∴
,∴![]()


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+4[sin(θ+![]() )]x﹣2,θ∈[0,2π].
)]x﹣2,θ∈[0,2π].
(Ⅰ)若函數f(x)為偶函數,求tanθ的值;
(Ⅱ)若f(x)在[﹣![]() ,1]上是單調函數,求θ的取值范圍.
,1]上是單調函數,求θ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年9月25日.阿里巴巴在杭州云棲大會上正式對外發布了含光800AI芯片,在業界標準的ResNet -50測試中,含光800推理性能達到78563lPS,比目前業界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在國內集成電路產業發展中,集成電路設計產業始終是國內集成電路產業中最具發展活力的領域,增長也最為迅速.如圖是2014-2018年中國集成電路設計產業的銷售額(億元)及其增速(%)的統計圖,則下面結論中正確的是( )
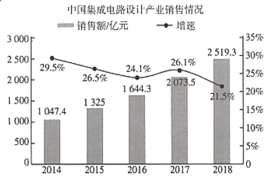
A.2014-2018年,中國集成電路設計產業的銷售額逐年增加
B.2014-2017年,中國集成電路設計產業的銷售額增速逐年下降
C.2018年中國集成電路設計產業的銷售額的增長率比2015年的高
D.2018年與2014年相比,中國集成電路設計產業銷售額的增長率約為110%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知O為坐標原點,拋物線E的方程為x2=2py(p>0),其焦點為F,過點M (0,4)的直線![]() 與拋物線相交于P、Q兩點且△OPQ為以O為直角頂點的直角三角形.
與拋物線相交于P、Q兩點且△OPQ為以O為直角頂點的直角三角形.
(Ⅰ)求E的方程;
(Ⅱ)設點N為曲線E上的任意一點,證明:以FN為直徑的圓與x軸相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節期間,我國高速公路繼續執行“節假日高速公路免費政策”某路橋公司為掌握春節期間車輛出行的高峰情況,在某高速公路收費點記錄了大年初三上午9:20~10:40這一時間段內通過的車輛數,統計發現這一時間段內共有600輛車通過該收費點,它們通過該收費點的時刻的頻率分布直方圖如下圖所示,其中時間段9:20~9:40記作區間![]() ,9:40~10:00記作
,9:40~10:00記作![]() ,10:00~10:20記作
,10:00~10:20記作![]() ,10:20~10:40記作
,10:20~10:40記作![]() .例如:10點04分,記作時刻64.
.例如:10點04分,記作時刻64.

(1)估計這600輛車在9:20~10:40時間段內通過該收費點的時刻的平均值(同一組中的數據用該組區間的中點值代表);
(2)為了對數據進行分析,現采用分層抽樣的方法從這600輛車中抽取10輛,再從這10輛車中隨機抽取4輛,設抽到的4輛車中,在9:20~10:00之間通過的車輛數為X,求X的分布列與數學期望;
(3)由大數據分析可知,車輛在每天通過該收費點的時刻T服從正態分布![]() ,其中
,其中![]() 可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,
可用這600輛車在9:20~10:40之間通過該收費點的時刻的平均值近似代替,![]() 可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
可用樣本的方差近似代替(同一組中的數據用該組區間的中點值代表),已知大年初五全天共有1000輛車通過該收費點,估計在9:46~10:40之間通過的車輛數(結果保留到整數).
參考數據:若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() 的左、右焦點分別為F1、F2,過點F1作圓x2+y2=a2的切線交雙曲線右支于點M,若tan∠F1MF2=2,又e為雙曲線的離心率,則e2的值為( )
的左、右焦點分別為F1、F2,過點F1作圓x2+y2=a2的切線交雙曲線右支于點M,若tan∠F1MF2=2,又e為雙曲線的離心率,則e2的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,將曲線方程![]() ,先向左平移2個單位,再向上平移2個單位,得到曲線C.
,先向左平移2個單位,再向上平移2個單位,得到曲線C.
(1)點M(x,y)為曲線C上任意一點,寫出曲線C的參數方程,并求出![]() 的最大值;
的最大值;
(2)設直線l的參數方程為![]() ,(t為參數),又直線l與曲線C的交點為E,F,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段EF的中點且與l垂直的直線的極坐標方程.
,(t為參數),又直線l與曲線C的交點為E,F,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段EF的中點且與l垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 和函數
和函數![]() ,關于這兩個函數圖像的交點個數,下列四個結論:①當
,關于這兩個函數圖像的交點個數,下列四個結論:①當![]() 時,兩個函數圖像沒有交點;②當
時,兩個函數圖像沒有交點;②當![]() 時,兩個函數圖像恰有三個交點;③當
時,兩個函數圖像恰有三個交點;③當![]() 時,兩個函數圖像恰有兩個交點;④當
時,兩個函數圖像恰有兩個交點;④當![]() 時,兩個函數圖像恰有四個交點.正確結論的個數為( )
時,兩個函數圖像恰有四個交點.正確結論的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com