
【題目】若函數![]() 滿足:對任意實數
滿足:對任意實數![]() 以及定義中任意兩數
以及定義中任意兩數![]() 、
、![]() (
(![]() ),恒有
),恒有![]() ,則稱
,則稱![]() 是下凸函數.
是下凸函數.
(1)證明:函數![]() 是下凸函數;
是下凸函數;
(2)判斷![]() 是不是下凸函數,并說明理由;
是不是下凸函數,并說明理由;
(3)若![]() 是定義在
是定義在![]() 上的下凸函數,常數
上的下凸函數,常數![]() ,滿足:
,滿足:![]() ,
,![]() ,且
,且![]() ,求證:
,求證:![]() ,并求
,并求![]() 在
在![]() 上的解析式.
上的解析式.
【答案】(1)證明見解析; (2) 不是;理由見解析; (3)證明見解析;![]()
【解析】
(1)根據定義,代入不等式作差證明不等式成立,即可證明函數![]() 是下凸函數.
是下凸函數.
(2)利用特殊值法, 令![]() 代入后檢驗不等式左右的大小,即可判斷不等式是否成立.
代入后檢驗不等式左右的大小,即可判斷不等式是否成立.
(3)根據極限定義,可求得當![]() 時
時![]() 的極限值;結合不等式
的極限值;結合不等式![]() ,
,![]() 即可求得
即可求得![]() 的值.進而利用賦值法求得
的值.進而利用賦值法求得![]() 上的解析式.
上的解析式.
(1)證明:對任意實數![]() 、
、![]() (
(![]() ),
), ![]()
有![]()
![]()
![]()
![]()
![]()
因為![]() ,實數
,實數![]() 、
、![]() (
(![]() )
)
所以![]()
即![]()
所以函數![]() 是下凸函數
是下凸函數
(2)![]() 不是下凸函數
不是下凸函數
理由如下:
![]()
則不等式左邊![]()
不等式右邊![]()
因為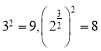 ,
,
所以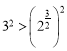 ,即
,即![]()
即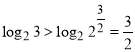
所以![]()
與定義![]() 矛盾
矛盾
所以![]() 不是下凸函數
不是下凸函數
(3)證明:因為![]() 是定義在
是定義在![]() 上的下凸函數,常數
上的下凸函數,常數![]() ,滿足:
,滿足:![]() ,
,![]() ,且
,且![]()
所以當![]() 時,
時, ![]()
而對于任意![]() ,
,![]()
所以![]()
而當![]() 時,由
時,由 ![]() 可得
可得![]()
綜上可知![]() ,即
,即![]()
得證.
根據下凸函數滿足![]() ,
,![]()
令![]()
代入可得![]()
而![]()
所以![]() ,
,![]()
又因為![]() ,
,![]()
所以當![]() 時
時![]()


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某旅游勝地欲開發一座景觀山,從山的側面進行勘測,迎面山坡線![]() 由同一平面的兩段拋物線組成,其中
由同一平面的兩段拋物線組成,其中![]() 所在的拋物線以
所在的拋物線以![]() 為頂點、開口向下,
為頂點、開口向下,![]() 所在的拋物線以
所在的拋物線以![]() 為頂點、開口向上,以過山腳(點
為頂點、開口向上,以過山腳(點![]() )的水平線為
)的水平線為![]() 軸,過山頂(點
軸,過山頂(點![]() )的鉛垂線為
)的鉛垂線為![]() 軸建立平面直角坐標系如圖(單位:百米).已知
軸建立平面直角坐標系如圖(單位:百米).已知![]() 所在拋物線的解析式
所在拋物線的解析式![]() ,
,![]() 所在拋物線的解析式為
所在拋物線的解析式為![]()
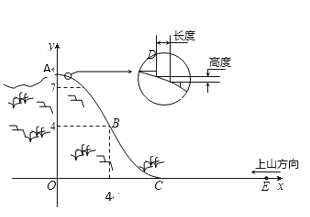
(1)求![]() 值,并寫出山坡線
值,并寫出山坡線![]() 的函數解析式;
的函數解析式;
(2)在山坡上的700米高度(點![]() )處恰好有一小塊平地,可以用來建造索道站,索道的起點選擇在山腳水平線上的點
)處恰好有一小塊平地,可以用來建造索道站,索道的起點選擇在山腳水平線上的點![]() 處,
處,![]() (米),假設索道
(米),假設索道![]() 可近似地看成一段以
可近似地看成一段以![]() 為頂點、開口向上的拋物線
為頂點、開口向上的拋物線![]() 當索道在
當索道在![]() 上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
上方時,索道的懸空高度有最大值,試求索道的最大懸空高度;
(3)為了便于旅游觀景,擬從山頂開始、沿迎面山坡往山下鋪設觀景臺階,臺階每級的高度為20厘米,長度因坡度的大小而定,但不得少于20厘米,每級臺階的兩端點在坡面上(見圖).試求出前三級臺階的長度(精確到厘米),并判斷這種臺階能否一直鋪到山腳,簡述理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在等腰梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四邊形
,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() .
.
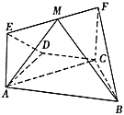
(1)求證:![]() 平面
平面![]() ;
;
(2)點![]() 在線段
在線段![]() 上運動,設平面
上運動,設平面![]() 與平面
與平面![]() 所成二面角的平面角為
所成二面角的平面角為![]() (
(![]() ),試求
),試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為調查高三年級學生的身高情況,按隨機抽樣的方法抽取100名學生,得到男生身高情況的頻率分布直方圖(圖(1))和女生身高情況的頻率分布直方圖(圖(2)).已知圖(1)中身高在![]() 的男生人數有16人.
的男生人數有16人.
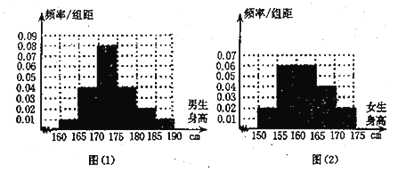
(1)試問在抽取的學生中,男,女生各有多少人?
(2)根據頻率分布直方圖,完成下列的![]() 列聯表,并判斷能有多大(百分之幾)的把握認為“身高與性別有關”?
列聯表,并判斷能有多大(百分之幾)的把握認為“身高與性別有關”?
|
| 總計 | |
男生身高 | |||
女生身高 | |||
總計 |
(3)在上述100名學生中,從身高在![]() 之間的男生和身高在
之間的男生和身高在![]() 之間的女生中間按男、女性別分層抽樣的方法,抽出6人,從這6人中選派2人當旗手,求2人中恰好有一名女生的概率.
之間的女生中間按男、女性別分層抽樣的方法,抽出6人,從這6人中選派2人當旗手,求2人中恰好有一名女生的概率.
參考公式:![]()
參考數據:
| 0.025 | 0.010 | 0.005 | 0.001 |
5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合![]() 是實數集
是實數集![]() 的子集,如果正實數
的子集,如果正實數![]() 滿足:對任意
滿足:對任意![]() 都存在
都存在![]() 使得
使得![]() 則稱
則稱![]() 為集合
為集合![]() 的一個“跨度”,已知三個命題:
的一個“跨度”,已知三個命題:
(1)若![]() 為集合
為集合![]() 的“跨度”,則
的“跨度”,則![]() 也是集合
也是集合![]() 的“跨度”;
的“跨度”;
(2)集合![]() 的“跨度”的最大值是4;
的“跨度”的最大值是4;
(3)![]() 是集合
是集合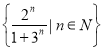 的“跨度”.
的“跨度”.
這三個命題中正確的個數是()
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2007年至2013年農村居民家庭純收入y(單位:千元)的數據如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關于t的線性回歸方程;
(2)利用(1)中的回歸方程,分析2007年至2013年該地區農村居民家庭人均純收入的變化情況,并預測該地區2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
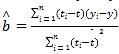 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(4,0)、B(1,0),動點M滿足|AM|=2|BM|.
(1)求動點M的軌跡C的方程;
(2)直線l:x+y=4,點N∈l,過N作軌跡C的切線,切點為T,求NT取最小時的切線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com