
【題目】在平面直角坐標系中,點![]() 是直線
是直線![]() 上的動點,定點
上的動點,定點![]() 點
點![]() 為
為![]() 的中點,動點
的中點,動點![]() 滿足
滿足![]() .
.
(1)求點![]() 的軌跡
的軌跡![]() 的方程
的方程
(2)過點![]() 的直線交軌跡
的直線交軌跡![]() 于
于![]() 兩點,
兩點,![]() 為
為![]() 上任意一點,直線
上任意一點,直線![]() 交
交![]() 于
于![]() 兩點,以
兩點,以![]() 為直徑的圓是否過
為直徑的圓是否過![]() 軸上的定點? 若過定點,求出定點的坐標;若不過定點,說明理由。
軸上的定點? 若過定點,求出定點的坐標;若不過定點,說明理由。
【答案】(1)![]() (2)以
(2)以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]()
【解析】分析:(1)根據條件可得點![]() 的軌跡是以
的軌跡是以![]() 為焦點、以直線
為焦點、以直線![]() 為準線的拋物線,其方程為
為準線的拋物線,其方程為![]() .(2)假設以
.(2)假設以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() , 設
, 設![]()
![]()
![]() .由題意可得
.由題意可得![]() ,
,![]() ,由
,由![]() 得
得![]() .設直線
.設直線![]() 的方程為
的方程為![]() ,與拋物線方程聯立消元后得到二次方程,結合根與系數的關系和上式可得
,與拋物線方程聯立消元后得到二次方程,結合根與系數的關系和上式可得![]() ,解得
,解得![]() ,進而可得以
,進而可得以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() .
.
詳解:(1)由已知得![]() 垂直平分
垂直平分![]() ,故
,故![]()
又![]() 軸,
軸,
則![]() ,
,
所以點![]() 到點
到點![]() 的距離和到直線
的距離和到直線![]() 的距離相等,
的距離相等,
故點![]() 的軌跡是以
的軌跡是以![]() 為焦點、以直線
為焦點、以直線![]() 為準線的拋物線,
為準線的拋物線,
由條件可得軌跡的方程為![]() .
.
(2)假設以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() .
.
設![]()
![]()
![]() ,
,
則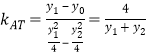 ,
,
直線![]() 的方程為
的方程為![]() ,
,
令![]() 得
得![]() 即
即![]() .
.
同理可得![]() .
.
由已知得![]() 恒成立,即
恒成立,即![]() ,
,
即![]() .
.
設直線![]() 的方程為
的方程為![]() ,
,
由![]() 消去
消去![]() 整理得
整理得![]() ,
,
所以![]() ,
,
于是![]() ,
,
整理得![]() ,
,
解得![]() .
.
故以![]() 為直徑的圓過
為直徑的圓過![]() 軸上的定點
軸上的定點![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ<![]() )的圖象與x軸的交點中,相鄰兩條對稱軸之間的距離為
)的圖象與x軸的交點中,相鄰兩條對稱軸之間的距離為![]() ,且圖象上一個最低點為M
,且圖象上一個最低點為M![]() .
.
(1)求ω,φ的值;
(2)求f(x)的圖像的對稱中心;
(3)當x∈![]() 時,求f(x)的值域.
時,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是線段BC,AB的中點.
,E,F是線段BC,AB的中點.

![]() Ⅰ
Ⅰ![]() 證明:
證明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在線段PA上確定點G,使得
在線段PA上確定點G,使得![]() 平面PED,請說明理由.
平面PED,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A、B、C三位老師分別教數學、英語、體育、勞技、語文、閱讀六門課,每位教兩門.已知:
(1)體育老師和數學老師住在一起,
(2)A老師是三位老師中最年輕的,
(3)數學老師經常與C老師下象棋,
(4)英語老師比勞技老師年長,比B老師年輕,
(5)三位老師中最年長的老師比其他兩位老師家離學校遠.
問:A、B、C三位老師每人各教哪幾門課?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四面體![]() 中,
中, ![]() 在平面
在平面![]() 的射影
的射影![]() 為棱
為棱![]() 的中點,
的中點, ![]() 為棱
為棱![]() 的中點,過直線
的中點,過直線![]() 作一個平面與平面
作一個平面與平面![]() 平行,且與
平行,且與![]() 交于點
交于點![]() ,已知
,已知![]() ,
, ![]() .
.

(1)證明: ![]() 為線段
為線段![]() 的中點
的中點
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:關于x的一元二次方程![]() 有兩個不相等的實數根;命題q:關于x的一元二次方程
有兩個不相等的實數根;命題q:關于x的一元二次方程![]() 對于任意實數a都沒有實數根.
對于任意實數a都沒有實數根.
![]() 若命題p為真命題,求實數m的取值范圍;
若命題p為真命題,求實數m的取值范圍;
![]() 若命題p和命題q中有且只有一個為真命題,求實數m的取值范圍.
若命題p和命題q中有且只有一個為真命題,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四面體P﹣ABC的外接球的球心O在AB上,且PO⊥平面ABC,2AC= ![]() AB,若四面體P﹣ABC的體積為
AB,若四面體P﹣ABC的體積為 ![]() ,則該球的體積為( )
,則該球的體積為( )
A.![]()
B.2π
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“開門大吉”是某電視臺推出的游戲節目.選手面對1~8號8扇大門,依次按響門上的門鈴,門鈴會播放一段音樂(將一首經典流行歌曲以單音色旋律的方式演繹),選手需正確回答出這首歌的名字,方可獲得該扇門對應的家庭夢想基金.在一次場外調查中,發現參賽選手多數分為兩個年齡段:20~30;30~40(單位:歲),其猜對歌曲名稱與否的人數如圖所示. 
(1)寫出2×2列聯表;判斷是否有90%的把握認為猜對歌曲名稱與否和年齡有關;說明你的理由;(下面的臨界值表供參考) (參考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
(2)現計劃在這次場外調查中按年齡段選取6名選手,并抽取3名幸運選手,求3名幸運選手中在20~30歲之間的人數的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com