解:(Ⅰ)當k=0時,f(x)=e
2x-1-2x,
f
′(x)=2e
2x-2,
令f
′(x)>0,則2e
2x-2>0,解得:x>0.
令f
′(x)<0,則2e
2x-2<0,解得:x<0.
所以,函數f(x)=e
2x-1-2x的單調增區間為(0,+∞).
單調減區間為(-∞,0).
(Ⅱ)由函數f(x)=e
2x-1-2x-kx
2,
則f
′(x)=2e
2x-2kx-2=2(e
2x-kx-1),
令g(x)=e
2x-kx-1,
則g
′(x)=2e
2x-k.
由x≥0,
所以,①當k≤2時,g
′(x)≥0,g(x)為增函數,而g(0)=0,
所以g(x)≥0,即f
′(x)≥0,所以f(x)在[0,+∞)上為增函數,
而f(0)=0,所以f(x)≥0在[0,+∞)上恒成立.
②當k>2時,令g
′(x)<0,即2e
2x-k<0,則0≤x<
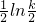
.
即g(x)在[0,
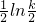
)上為減函數,而g(0)=0,所以,g(x)在[0,
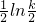
)上小于0.
即f
′(x)<0,所以,f(x)在[0,
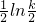
)上為減函數,而f(0)=0,故此時f(x)<0,不合題意.
綜上,k≤2.
(Ⅲ)
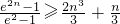
.
事實上,由(Ⅱ)知,f(x)=e
2x-1-2x-2x
2在[0,+∞)上為增函數,
所以,e
2x≥2x
2+2x+1=x
2+(x+1)
2,
則e
0≥1
2e
2≥1
2+2
2e
4≥2
2+3
2e
6≥3
2+4
2…
e
2(n-1)≥(n-1)
2+n
2累加得:1+e
2+e
4+e
6+…+e
2(n-1)≥2(1
2+2
2+3
2+…+(n-1)
2)+n
2.
即
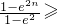
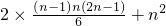
.
所以,
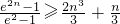
.
分析:(Ⅰ)取x=0后,求出函數的導函數,由導函數大于0和導函數小于0分別求出函數的單調區間;
(Ⅱ)求出原函數的導函數,以k≤2和k>2進行分類討論,由k≤2時,說明原函數在[0,+∞)上為增函數,說明f(x)≥0在[0,+∞)上恒成立,k>2時,說明這種情況不存在;
(Ⅲ)結合(Ⅱ),說明函數f(x)當k=2時為增函數,把不等式變形e
2x≥2x
2+2x+1=x
2+(x+1)
2后,依次取x的值為0,1,2…,(n-1),累加后利用等比數列求和公式可得結論.
點評:本題考查了利用導函數研究函數的單調性,考查了函數中的恒成立問題,考查了不等式的證明,解答此題的關鍵是運用導函數分析函數的單調性,同時考查了學生靈活的變式思維能力,此題屬難題.

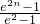 與
與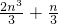 (n為任意非負整數)的大小關系,并給出證明.
(n為任意非負整數)的大小關系,并給出證明.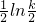 .
.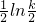 )上為減函數,而g(0)=0,所以,g(x)在[0,
)上為減函數,而g(0)=0,所以,g(x)在[0,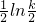 )上小于0.
)上小于0.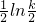 )上為減函數,而f(0)=0,故此時f(x)<0,不合題意.
)上為減函數,而f(0)=0,故此時f(x)<0,不合題意.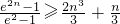 .
.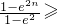
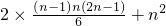 .
.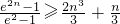 .
.

 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案