
【題目】如圖,在三棱柱![]() 中,
中,![]() 分別是
分別是![]() 的中點.
的中點.
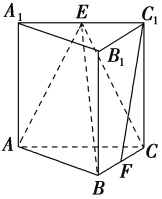
(1)求證:![]() 平面
平面![]() ;
;
(2)過點![]() 作一個截面
作一個截面![]() ,使平面
,使平面![]() 平面
平面![]() ,并證明.
,并證明.
科目:高中數學 來源: 題型:
【題目】如圖,在同一個平面內,向量 ![]() ,
, ![]() ,
, ![]() 的模分別為1,1,
的模分別為1,1, ![]() ,
, ![]() 與
與 ![]() 的夾角為α,且tanα=7,
的夾角為α,且tanα=7, ![]() 與
與 ![]() 的夾角為45°.若
的夾角為45°.若 ![]() =m
=m ![]() +n
+n ![]() (m,n∈R),則m+n= .
(m,n∈R),則m+n= . 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若橢圓的中心在原點,焦點在![]() 軸上,點
軸上,點![]() 是橢圓上的一點,
是橢圓上的一點,![]() 在
在![]() 軸上的射影恰為橢圓的左焦點,
軸上的射影恰為橢圓的左焦點,![]() 與中心
與中心![]() 的連線平行于右頂點與上頂點的連線,且左焦點與左頂點的距離等于
的連線平行于右頂點與上頂點的連線,且左焦點與左頂點的距離等于![]() ,試求橢圓的離心率及其方程.
,試求橢圓的離心率及其方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)當a=1時,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一種設備的單價為![]() 元,設備維修和消耗費用第一年為
元,設備維修和消耗費用第一年為![]() 元,以后每年增加
元,以后每年增加![]() 元(
元(![]() 是常數).用
是常數).用![]() 表示設備使用的年數,記設備年平均費用為
表示設備使用的年數,記設備年平均費用為![]() ,即
,即![]() (設備單價
(設備單價![]() 設備維修和消耗費用)
設備維修和消耗費用)![]() 設備使用的年數.
設備使用的年數.
(Ⅰ)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(Ⅱ)當![]() ,
, ![]() 時,求這種設備的最佳更新年限.
時,求這種設備的最佳更新年限.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 中,
中,![]() 在直線
在直線![]() .
.
(1)求數列{an}的通項公式;
(2)令![]() ,數列
,數列![]() 的前n項和為
的前n項和為![]() .
.
(ⅰ)求![]() ;
;
(ⅱ)是否存在整數λ![]() ,使得不等式(-1)nλ<
,使得不等式(-1)nλ<![]() (n∈N
(n∈N![]() )恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
)恒成立?若存在,求出λ的取值的集合;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設A,B為曲線C:y= ![]() 上兩點,A與B的橫坐標之和為4.(12分)
上兩點,A與B的橫坐標之和為4.(12分)
(1)求直線AB的斜率;
(2)設M為曲線C上一點,C在M處的切線與直線AB平行,且AM⊥BM,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() sin(ωx﹣
sin(ωx﹣ ![]() )+b(ω>0),且函數圖象的對稱中心到對稱軸的最小距離為
)+b(ω>0),且函數圖象的對稱中心到對稱軸的最小距離為 ![]() ,當x∈[0,
,當x∈[0, ![]() ]時,f(x)的最大值為1.
]時,f(x)的最大值為1.
(1)求函數f(x)的解析式;
(2)將函數f(x)的圖象向右平移 ![]() 個單位長度得到函數g(x)圖象,若g(x)﹣3≤m≤g(x)+3在x∈[0,
個單位長度得到函數g(x)圖象,若g(x)﹣3≤m≤g(x)+3在x∈[0, ![]() ]上恒成立,求實數m的取值范圍.
]上恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com